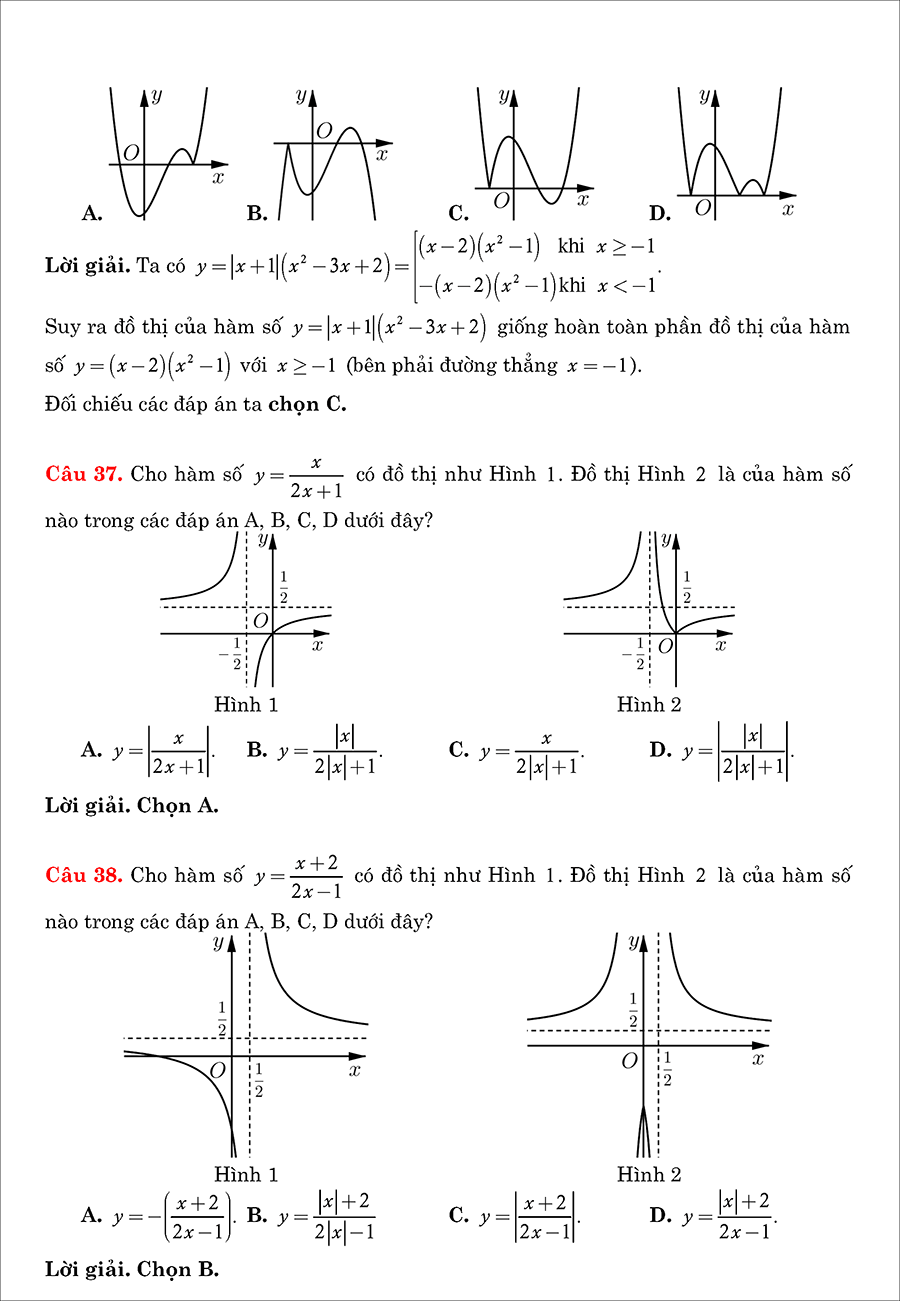
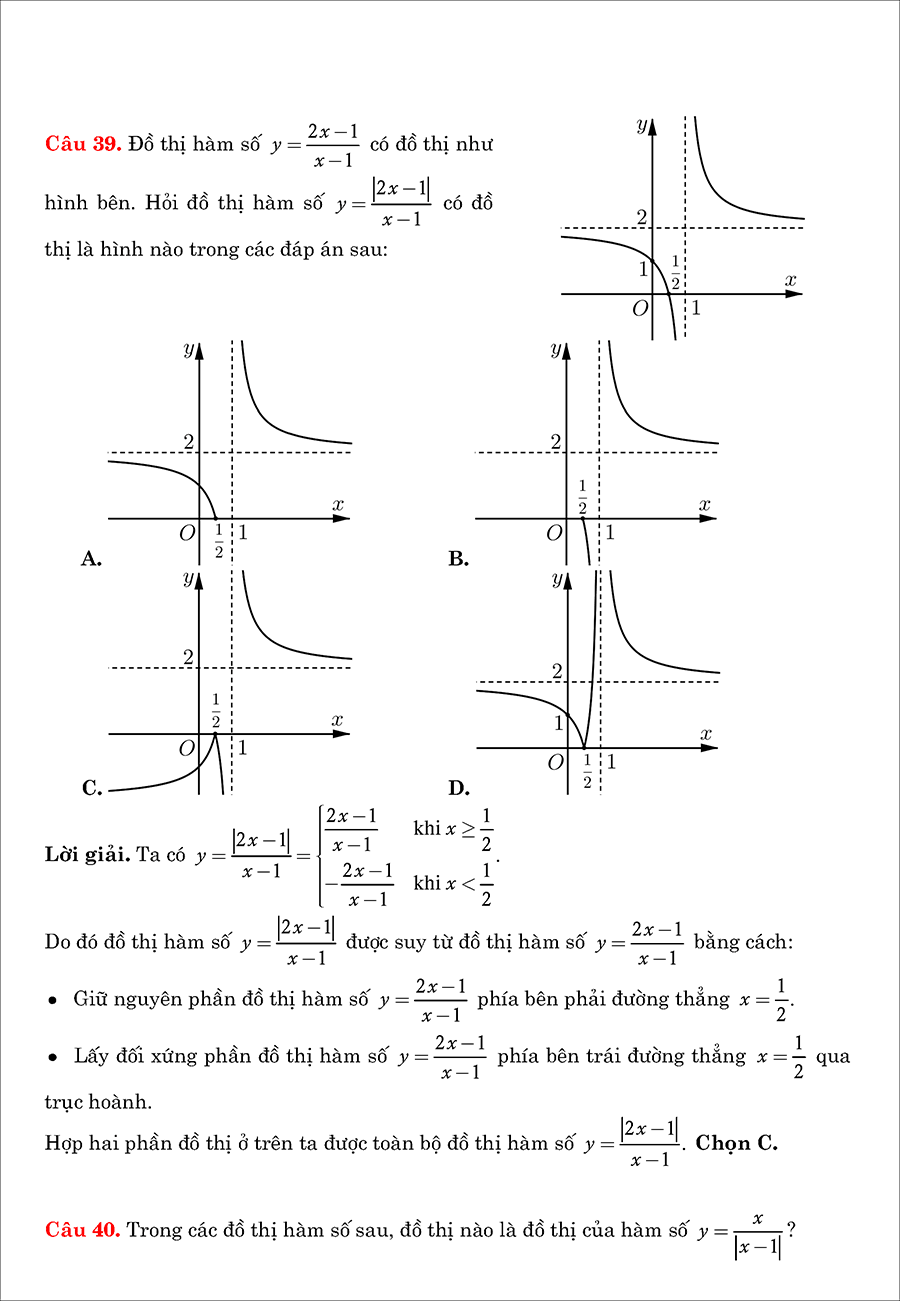
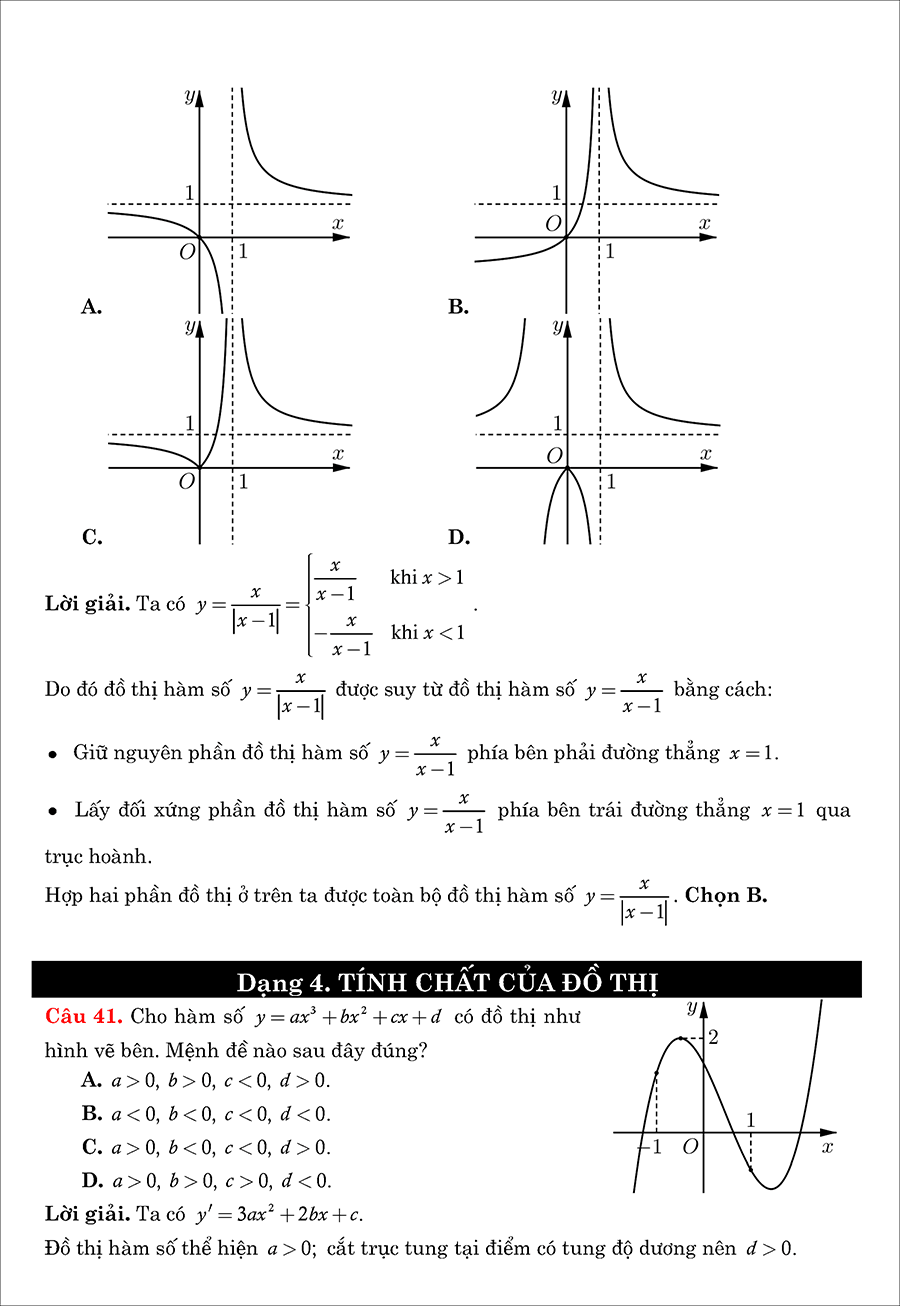
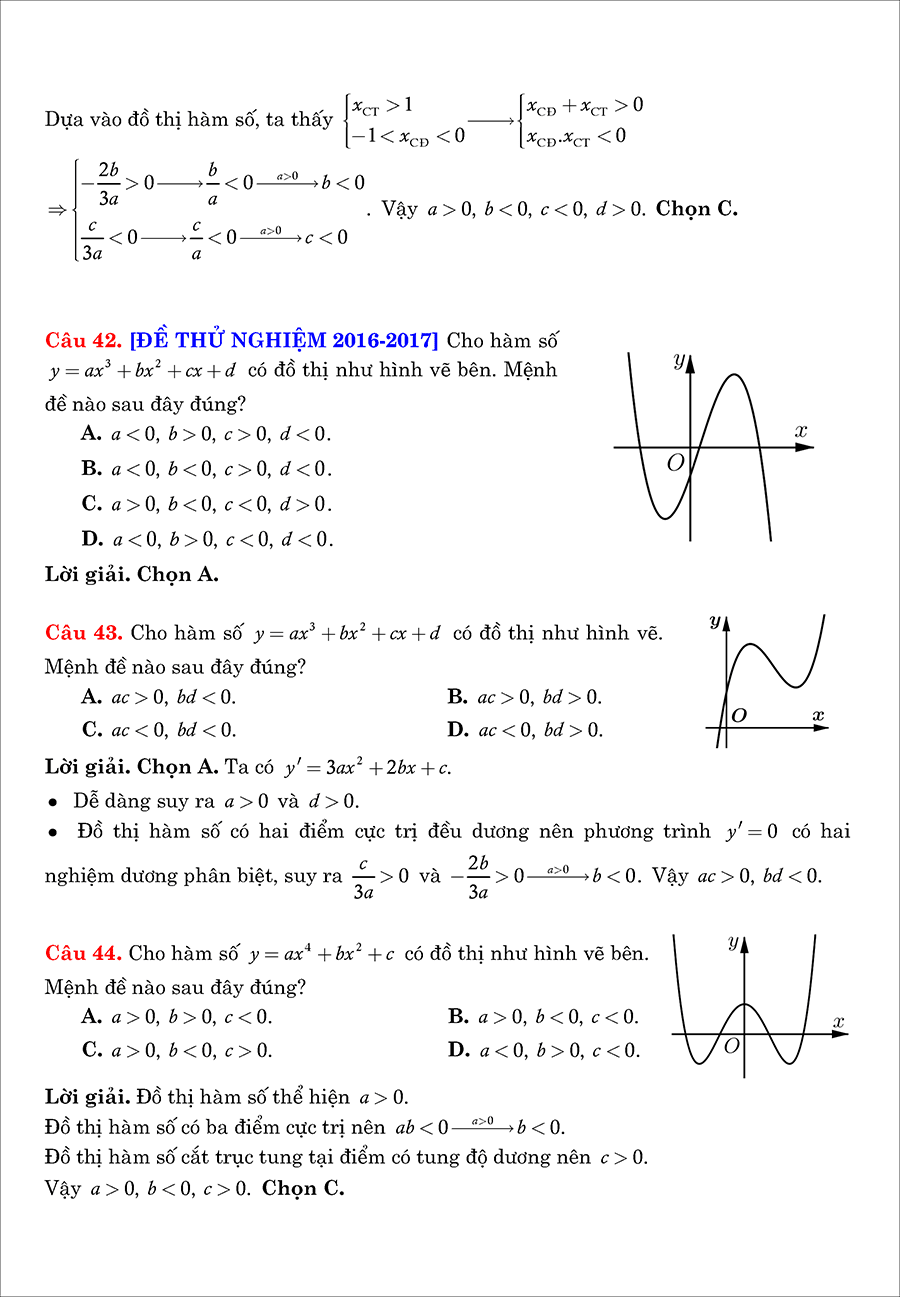
Chuyên đề khảo sát sự biến thiên và vẽ đồ thị hàm số thuộc chương trình toán lớp 12. Bài viết này chúng ta sẽ điểm qua 3 dạng đồ thị cơ bản nhất gồm: Hàm số bậc 3, hàm phân thức, hàm trùng phương. Mỗi dạng đồ thị sẽ đều có ví dụ và bài tập tự luyện cơ bản.
Dạng 1: Khảo sát sự biến thiên hàm số y = ax3 + bx2 + cx + d
#1.Tập xác định: D = ℝ
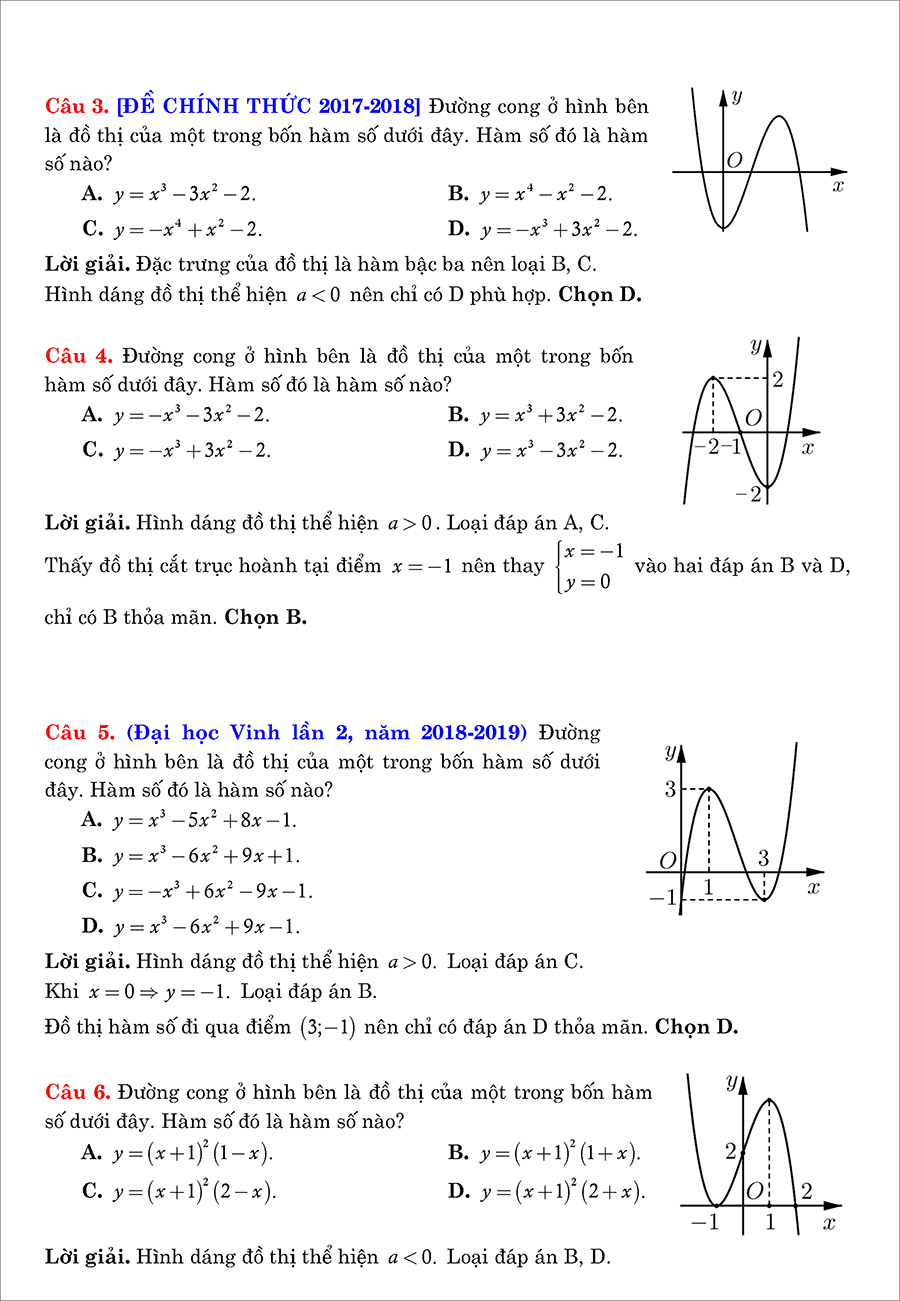
Tính y’ và cho y’ = 0 ⇒ các nghiệm (nếu có)
Tính các giới hạn:
#2. Lập bảng biến thiên
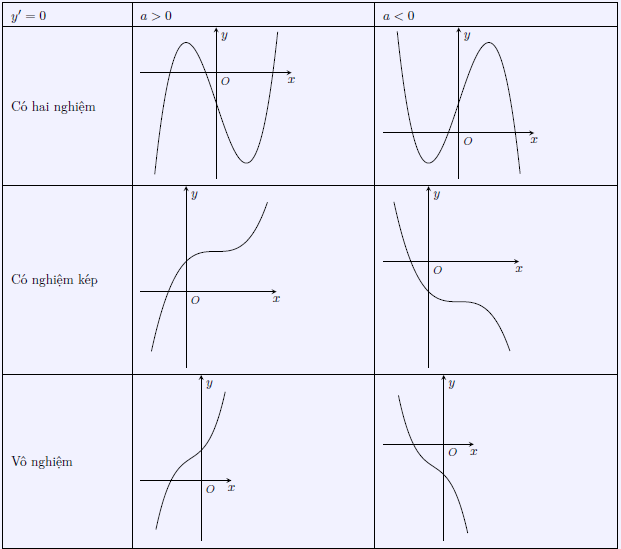
- Nếu y’ = 0 có hai nghiệm thì dấu của y’ là: “trong trái ngoài cùng”
- Nếu y’ = 0 có nghiệm kép thì dấu của y’ là: “luôn cùng dấu với a” ngoại trừ tại nghiệm kép.
- Nếu y’ = 0 vô nghiệm thì dấu của y’ là: “luôn cùng dấu với a”
#3. Kết luận
Tính chất đơn điệu của hàm số.
Cực trị hàm số
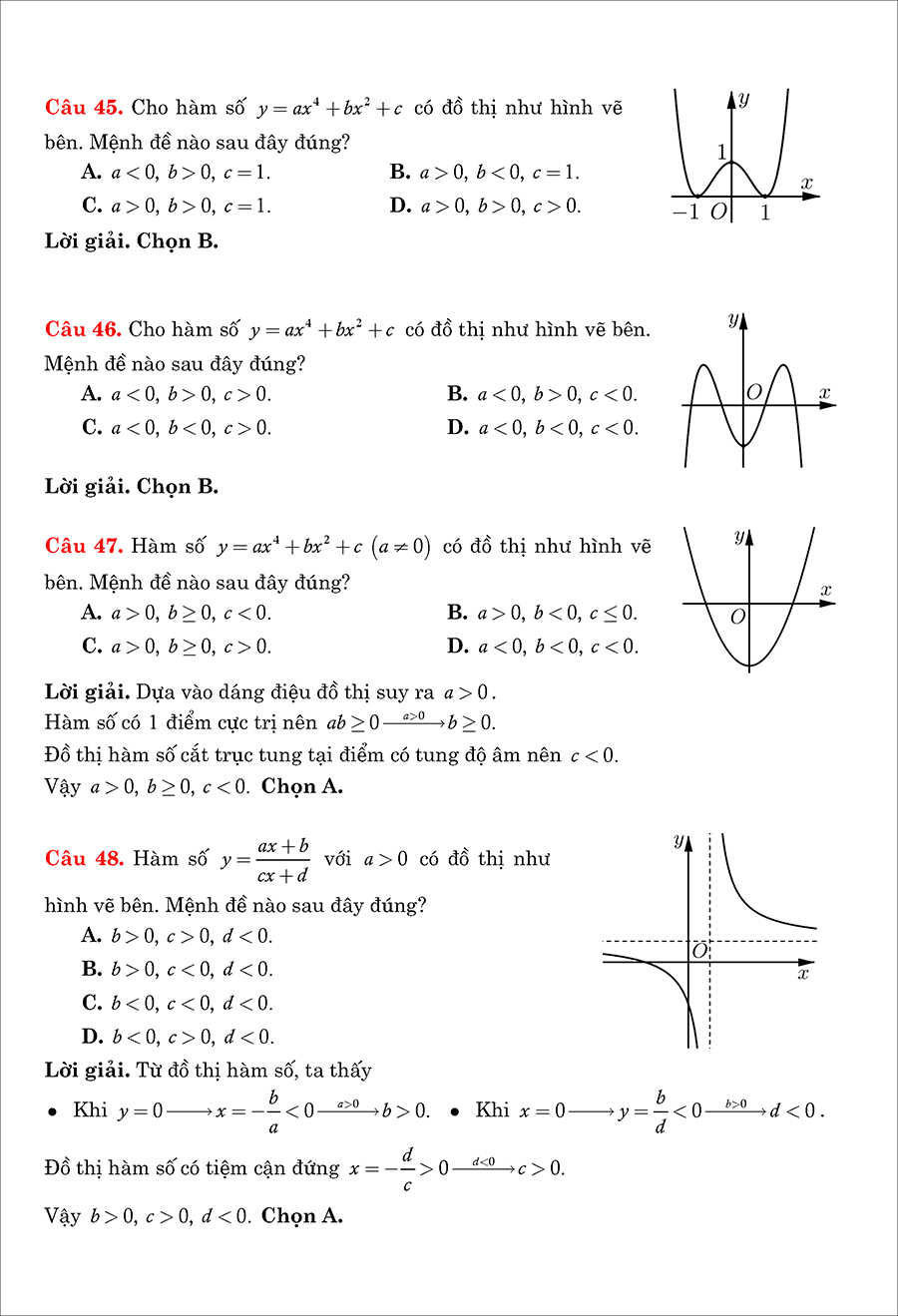
Chọn vài điểm đặc biệt vẽ đồ thị hàm số. Đồ thị có 6 dạng như sau:
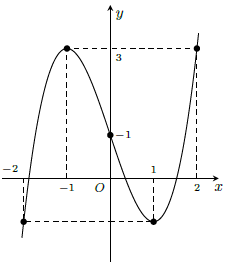
Ví dụ 1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số y = x3 − 3x + 1.
Lời giải.
Tập xác định: D = ℝ; y’ = 3x2 − 3
y’ = 0 ⇔
Từ bảng biến thiên:
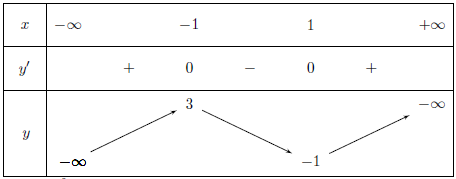
Hàm số đồng biến trên các khoảng (-∞; -1) và (1; +∞), nghịch biến trên khoảng (-1; 1)
Hàm số đạt cực đại tại x = -1; yCĐ = 3, hàm số đạt cực tiểu tại x = 1; yCĐ = -1.
Đồ thị hàm số đi qua các điểm: (-2; -1), (-1; 3), (0; 1), (1; -1), (2; 3)
Dạng 2: Khảo sát sự biến thiên và vẽ đồ thị hàm số y = ax4 + bx2 + c
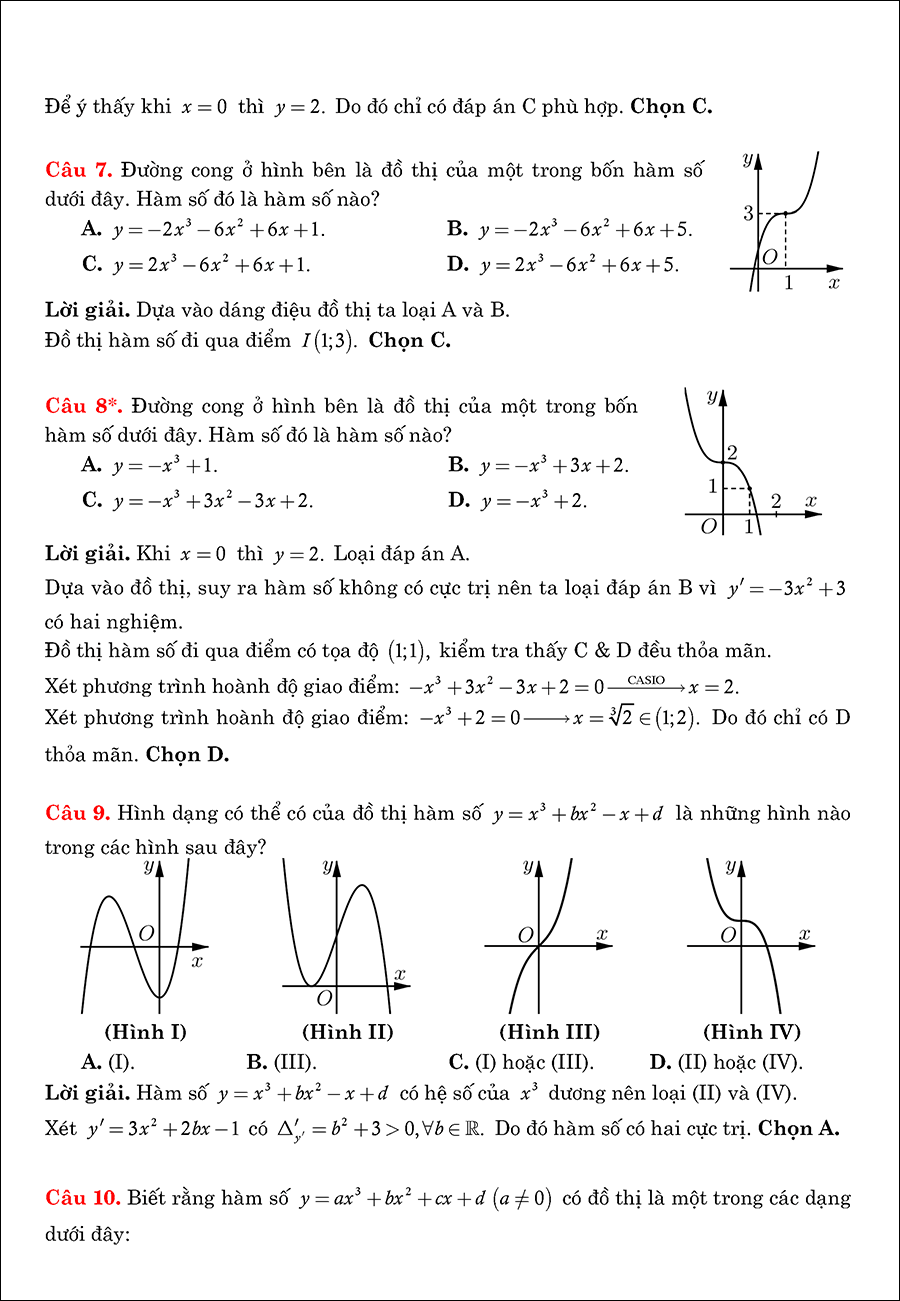
Tập xác định: D = ℝ
Tính y’ và cho y’ = 0 (có 3 có nghiệm hoặc có 1 nghiệm và luôn có 1 nghiệm x = 0).
Tính giới hạn:
Lập bảng biến thiên: “Bên phải bảng biến thiên, dấu y’ luôn cùng dấu với a”.
Kết luận:
Tính chất đơn điệu.
Cực trị hàm số.
Giới hạn của hàm số.
Vẽ đồ thị: Chọn vài điểm đặc biệt vẽ đồ thị hàm số
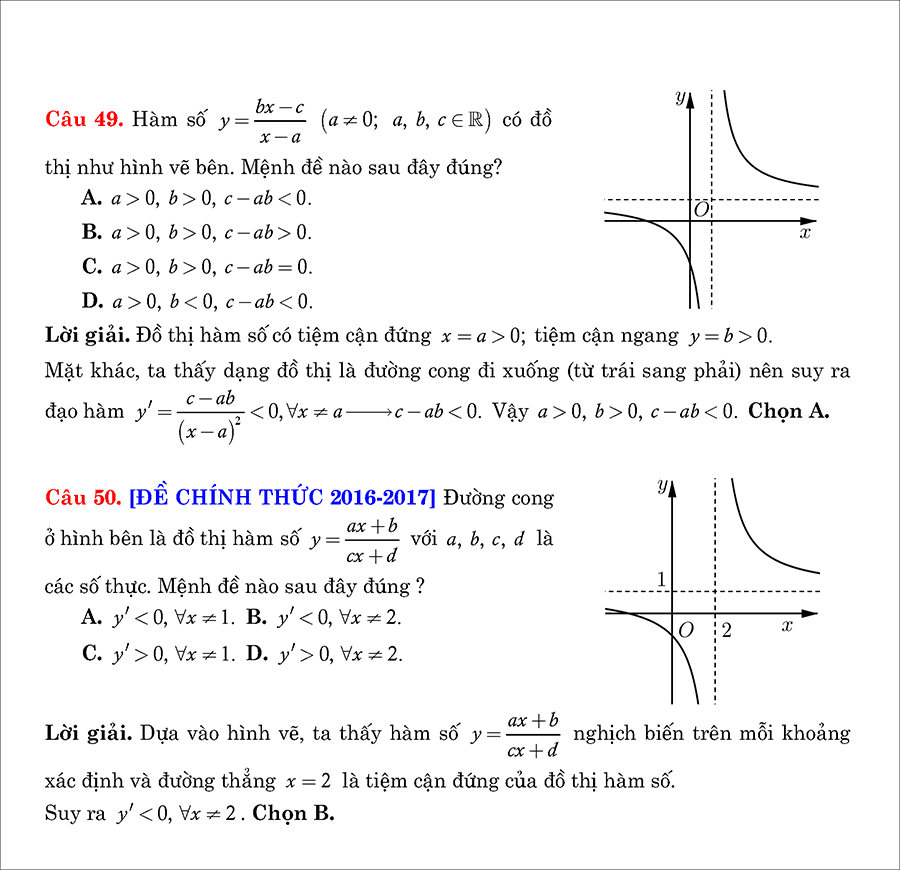
Đồ thị hàm số có 4 dạng sau:
Ví dụ 1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Lời giải.
Tập xác định: D = ℝ
y’ = x3 − x;
y’ = 0 ⇔
Từ bảng biến thiên:
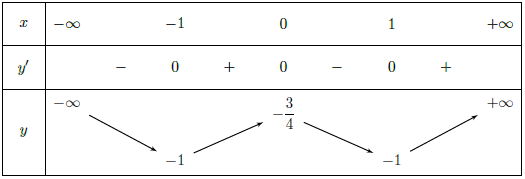
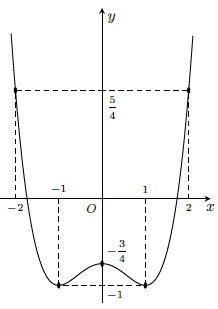
Hàm số đồng biến trên các khoảng (-1; 0) và (1; +∞), nghịch biến trên các khoảng (-∞; -1) và (0; 1).
Hàm số đạt cực đại tại x = 0 và yCĐ =
, đạt cực tiểu tại x = ±1 và yCT = -1.
Đồ thị hàm số đi qua các điểm
Dạng 3: Khảo sát sự biến thiên và vẽ đồ thị hàm số 

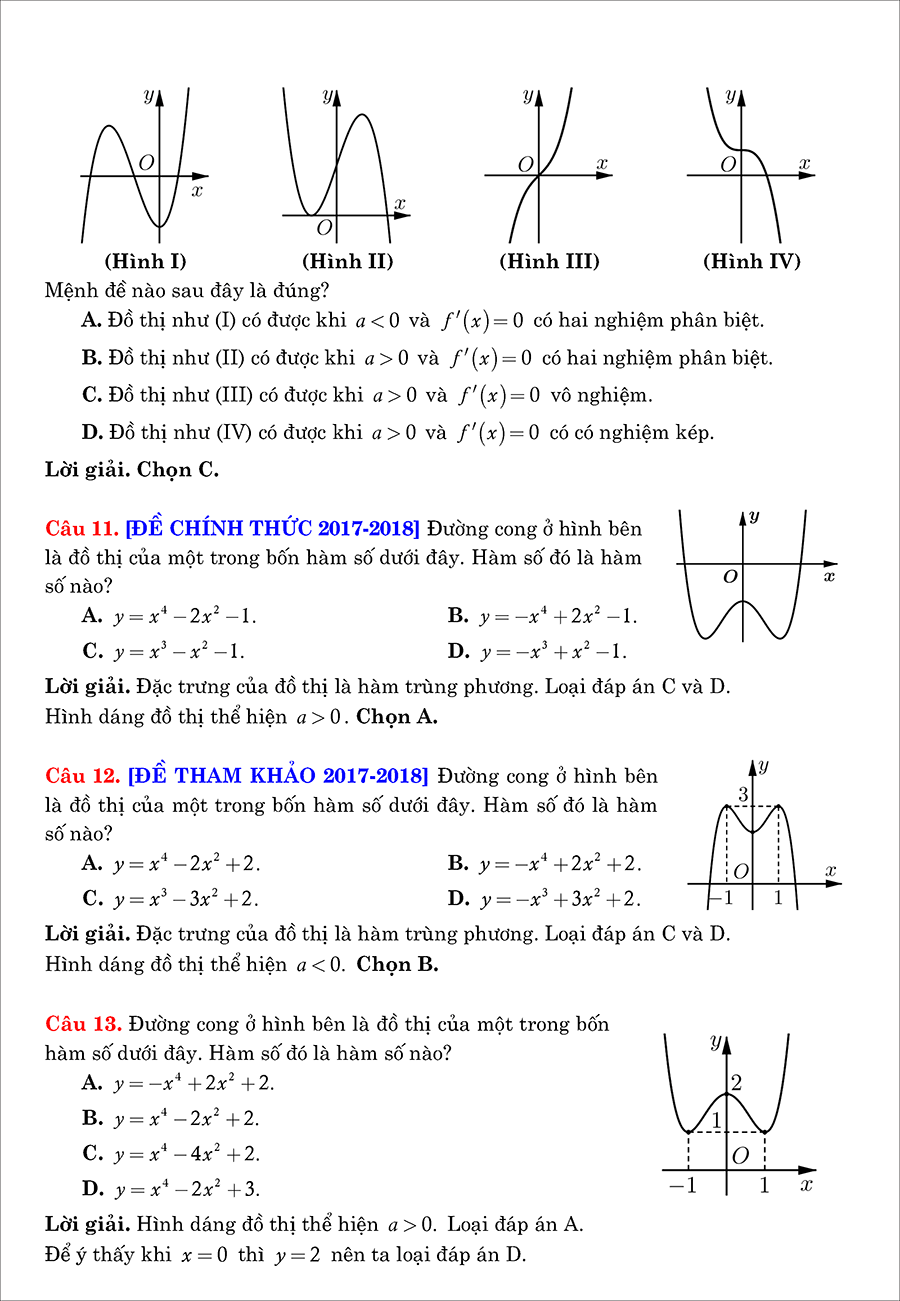
Tập xác định:
Tính
(y’ hoặc dương hoặc âm ∀ x ∈ D)
Đường tiệm cận:
Tiệm cận đứng:
vì
và
Tiệm cận ngang:
vì
Lập bảng biến thiên: Khi x → ±∞, thì
Kết luận:
Hàm số luôn đồng biến trên từng khoảng xác định hoặc luôn nghịch biến trên từng khoảng xác định.
Vẽ đồ thị: Đồ thị có 2 dạng và luôn luôn nhận giao điểm của hai đường tiệm cận là tâm đối xứng.
Vẽ đồ thị: Lấy thêm vài điểm đặc biệt.
Đồ thị có 2 dạng sau:
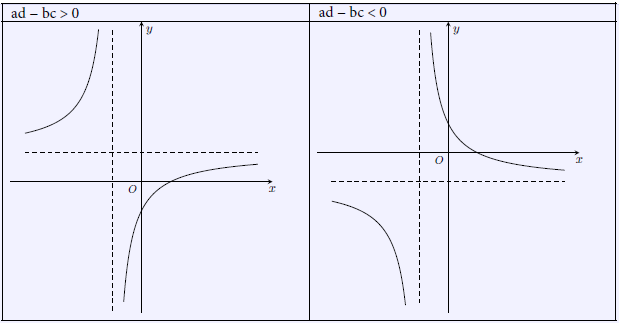
Ví dụ 1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số
Lời giải.
Tập xác định: D = ℝ {-1}
, ∀ x ∈ D.
Bảng biến thiên
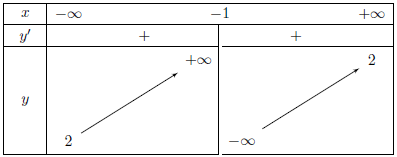
Hàm số đồng biến trên các khoảng (-∞; -1) và (-1; +∞) và không có cực trị.
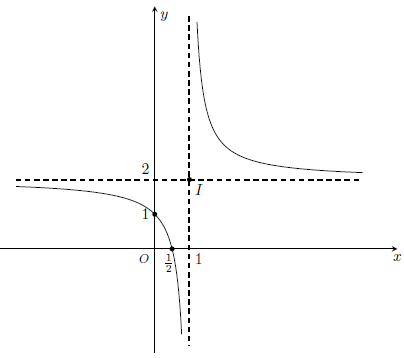
Đồ thị: Đồ thị hàm số qua các điểm (0; -1),
và nhận I(-1; 2) làm tâm đối xứng.
Tài liệu về khảo sát hàm số và vẽ đồ thị
Tài liệu xoay quanh 4 dạng toán cơ bản sau đây:
- Dạng 1: Đồ thị của hàm số
- Dạng 2: Bảng biến thiên
- Dạng 3: Phép suy của đồ thị
- Dạng 4: Tính chất của đồ thị hàm số