Cực trị hàm số là một mảng kiến thức khá quan trọng của chuyên đề hàm số thuộc chương trình toán lớp 12. và ứng dụng thi đại học. Xem thêm nhiều dạng bài tập và điểm lý thuyết khó trong bài viết sau đây sẽ giúp bạn hiểu hơn về mảng kiến thức này.
Lý thuyết cực trị của hàm số
Cực trị của hàm số là điểm có giá trị lớn nhất so với xung quanh và giá trị nhỏ nhất so với xung quanh mà hàm số có thể đạt được. Trong hình học, nó biểu diễn khoảng cách lớn nhất từ điểm này sang điểm kia và khoảng cách nhỏ nhất từ điểm này sang điểm nọ. Đây là khái niệm cơ bản về cực trị của hàm số.
Định nghĩa
Giả sử hàm số f xác định trên K (K ⊂ ℝ) và x0 ∈ K
a) x0 được gọi là điểm cực đại của hàm số f nếu tồn tại một khoảng (a;b) ⊂ K chứa điểm x0 sao cho f(x) < f(x0), ∀ x ∈ (a;b) {x0}
→ Khi đó f(x0) được gọi là giá trị cực đại của hàm số f.
b) x0 được gọi là điểm cực tiểu của hàm số f nếu tồn tại một khoảng (a;b) ⊂ K chứa điểm x0 sao cho f(x) > f(x0), ∀ x ∈ (a;b) {x0}
→ Khi đó f(x0) được gọi là giá trị cực tiểu của hàm số f.
Chú ý:
1) Điểm cực đại (cực tiểu) x0 được gọi chung là điểm cực trị. Giá trị cực đại (cực tiểu) f(x0) của hàm số được gọi chung là cực trị. Hàm số có thể đạt cực đại hoặc cực tiểu tại nhiều điểm trên tập hợp K.
2) Nói chung, giá trị cực đại (cực tiểu) f(x0) không phải là giá trị lớn nhất (nhỏ nhất) của hàm số f trên tập K; f(x0) chỉ là giá trị lớn nhất (nhỏ nhất) của hàm số f trên một khoảng (a;b) chứa x0.
3) Nếu x0 là một điểm cực trị của hàm số f thì điểm (x0; f(x0)) được gọi là điểm cực trị của đồ thị hàm số f.
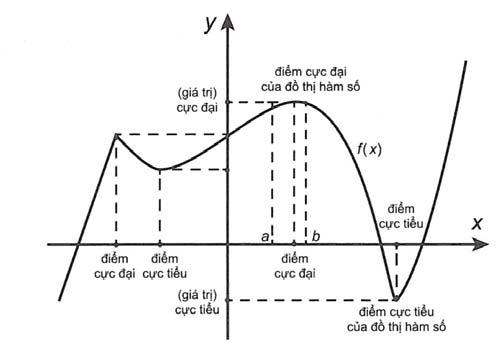
Điều kiện cần để hàm số đạt cực trị:
Định lí 1
Giả sử hàm số f đạt cực trị tại điểm x0. Khi đó, nếu f có đạo hàm tại điểm x0 thì f’(x0) = 0.
Chú ý:
1) Điều ngược lại có thể không đúng. Đạo hàm f’ có thể bằng 0 tại điểm x0 nhưng hàm số f không đạt cực trị tại điểm x0.
2) Hàm số có thể đạt cực trị tại một điểm mà tại đó hàm số không có đạo hàm.
Điều kiện đủ để hàm số đạt cực trị
Định lí 2
a) Nếu f’(x) đổi dấu từ âm sang dương khi x đi qua điểm x0 (theo chiều tăng) thì hàm số đạt cực tiểu tại x0.
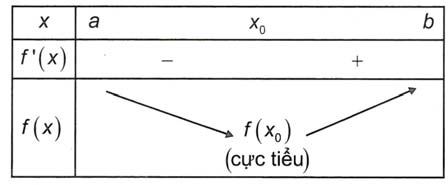
b) Nếu f’(x) đổi dấu từ dương sang âm khi x đi qua điểm x0 (theo chiều tăng) thì hàm số đạt cực đại tại x0.
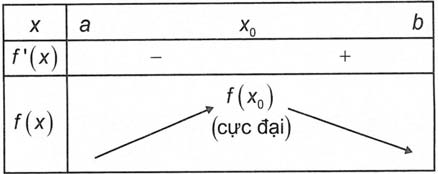
Định lí 3
Giả sử hàm số f có đạo hàm cấp một trên khoảng (a;b) chứa điểm x0, f’(x0) = 0 và f có đạo hàm cấp hai khác 0 tại điểm x0.
a) Nếu f’’(x0) < 0 thì hàm số f đạt cực đại tại điểm x0.
b) Nếu f’’(x0) > 0 thì hàm số f đạt cực tiểu tại điểm x0.
c) Nếu f’’(x0) = 0 thì ta chưa thể kết luận được, cần lập bảng biến thiên hoặc bảng xét dấu đạo hàm.
Phân dạng bài tập cơ bản về cực trị hàm số
Dạng 1: Tính đạo hàm để tìm cực trị của hàm số y = f(x)
Phương pháp:
Quy tắc I
- Tìm tập xác định.
- Tính y’ = f’(x). Tìm x khi f’(x) = 0 hoặc f’(x) không xác định.
- Tính các giới hạn cần thiết.
- Lập bảng biến thiên.
- Kết luận các điểm cực trị.
Quy tắc II
- Tìm tập xác định.
- Tính y’ = f’(x). Giải phương trình f’(x) = 0 để tìm các nghiệm x1, x2,… (nếu có) của nó.
- Tính f’’(x) và suy ra f’’(x1), f’’(x2),…
- Dựa vào dấu f’’(x1), f’’(x2),… để kết luận.
Ghi nhớ: Quy tắc II không dùng được trong trường hợp f’(x) = 0 vô nghiệm hoặc
Ví dụ 1. Cho hàm số y = x4 – 2x2 + 1 có bao nhiêu điểm cực trị?
A. 2
B. 3
C. 1
D. 0
Lời giải:
Chọn B
Tập xác định: D = ℝ.
Đạo hàm: y’ = 4x3 – 4x = 4x (x2 – 1)
y’ = 0
Giới hạn:
Bảng biến thiên:
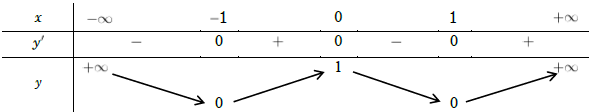
Ta thấy: Hàm số đạt cực tiểu tại x = ±1, giá trị cực tiểu là yCT = 0; hàm số đạt cực đại tại x = 0, giá trị cực đại là yCĐ = 1. Do đó hàm số có ba cực trị.
Ví dụ 2. Tìm điểm cực đại x0 của hàm số y = x3 – 3x +1.
A. x0 = 2
B. x0 = 1
C. x0 = -1
D. x0 = 3
Lời giải:
Chọn C
Tập xác định: D = ℝ.
Đạo hàm: y’ = 3x2 – 3
y’ = 0
Giới hạn:
Bảng biến thiên:
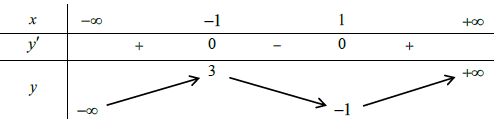
Dựa vào bảng biến thiên, ta thấy hàm số đạt cực đại tại x0 = -1.
Ví dụ 3. Hàm số  có bao nhiêu cực trị?
có bao nhiêu cực trị?
A. 3
B. 0
C. 2
D. 1
Lời giải:
Chọn B
Tập xác định: D = ℝ {2}
Ta có
Giới hạn
Bảng biến thiên:

Ta thấy hàm số đã cho không có cực trị.
Dạng 2: Tìm cực trị của hàm số dựa vào bảng biến thiên hoặc đạo hàm (cho sẵn).
Một số tính chất cần lưu ý
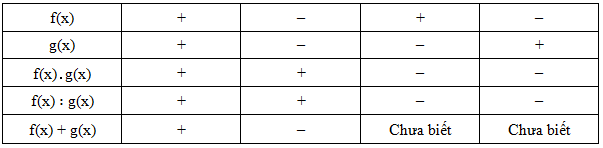
Cho hàm số f(x), g(x) cùng có đạo hàm trên tập D. Khi đó:
– [k․f(x)]’ = k․f’(x) với k là hằng số
– [f(x)․g(x)]’ = f’(x)․g(x) + f(x)․g’(x)
– [f(u)]’ = u’․f’(u)
– [f(x) ± g(x)]’ = f’(x) ± g’(x)
–
– y = f(x)
y = f(u)
Phương pháp chung
– Đặt g(x) là hàm số cần xét, ta tính đạo hàm g’(x).
– Kết hợp các nguyên tắc xét dấu tích, thương, tổng (hiệu) các biểu thức để có được bảng xét dấu cho g’(x).
– Dựa vào bảng xét dấu dành cho g’(x) để kết luận về cực trị của hàm số.
– Nhắc lại quy tắc về dấu của tích, thương, tổng (hiệu) các biểu thức:
Ví dụ 1. Cho hàm số y = f(x) xác định, liên tục trên và có bảng biến thiên
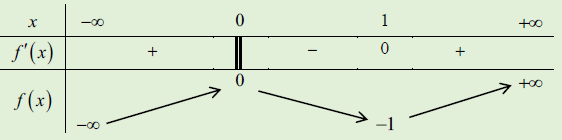
Khẳng định nào sau đây là khẳng định đúng?
A. Hàm số y = f(x) có giá trị cực tiểu bằng 1
B. Hàm số y = f(x) có giá trị lớn nhất bằng 0 và giá trị nhỏ nhất bằng 1
C. Hàm số y = f(x) đạt cực đại tại x = 0 và đạt cực tiểu tại x = 1
D. Hàm số y = f(x) có đúng một cực trị
Lời giải:
Chọn C
Dựa vào bảng biến thiên, ta thấy hàm số đạt cực tiểu tại điểm x = 1
Tại x = 0 mặc dù đạo hàm f’(x) không tồn tại nhưng hàm số f(x) vẫn xác định và liên tục nên hàm số đạt cực đại tại x = 0.
Ví dụ 2. Cho hàm số y = f(x) có bảng biến thiên:

Khẳng định nào sau đây sai?
A. Hàm số y = f(x) nghịch biến trên khoảng (0;4)
B. Hàm số y = f(x) đạt cực đại tại điểm x = 0
C. Hàm số y = f(x) đồng biến trên các khoảng (-∞; 0) và (4; +∞)
D. Hàm số y = f(x) có hai điểm cực trị
Lời giải:
Chọn D
Tại x = 0 dù đạo hàm không xác định nhưng hàm số y = f(x) vẫn xác định và liên tục nên hàm số đạt cực đại tại x = 0. Tại x = 4 thì hàm số y = f(x) không xác định, vì vậy hàm số không có cực trị tại x = 4.
Do đó hàm số chỉ có duy nhất một cực trị.
Ví dụ 3. Cho đồ thị (C) của hàm số y = f(x) có y’ = (1 + x)(x + 2)2(x – 3)3(1 – x2). Trong các mệnh đề sau, tìm mệnh đề đúng:
A. (C) có một điểm cực trị
B. (C) có hai điểm cực trị
C. (C) có ba điểm cực trị
D. (C) có bốn điểm cực trị
Lời giải:
Chọn B
Xét đạo hàm: y’ = (1 + x)(x + 2)2(x – 3)3(1 – x2) = (1 + x)2(x + 2)2(x – 3)3(1 – x)
y’ = 0
Vì x = -1, x = -2 là các nghiệm kép của y’ nên y’ không đổi dấu khi qua hai điểm này; x = 1, x = 3 là nghiệm kép của y’ nên y’ đổi dấu khi qua các điểm x = 1, x = 3.
Do đó hàm số có hai điểm cực trị x = 1, x = 3.
Cần nhớ: Cho n là số nguyên dương.
![]()
⇔ (x – x1)2 = 0 ⇔ x = x1 (ta nói x1 là nghiệm kép của phương trình).
![]()
⇔ (x – x2)1 = 0 ⇔ x = x2 (ta nói x2 là nghiệm đơn của phương trình).
Ví dụ 4. Cho hàm số y = f(x) có đạo hàm trên ℝ và có bảng xét dấu f’(x) như sau
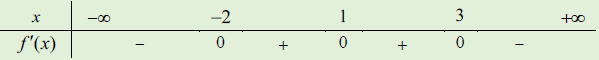
Hỏi hàm số y = f (x2 – 2x) có bao nhiêu điểm cực tiểu?
A. 4
B. 2
C. 3
D. 1
Lời giải:
Chọn D
Đặt g(x) = f (x2 – 2x)
Ta có g’(x) = (2x – 2)․f’(x2 – 2x)
Xét g’(x) ≥ 0 ⇔ (2x – 2)․f’(x2 – 2x) ≥ 0
Hợp nghiệm của (*), (**) ta có g’(x) ≥ 0
Do đó g’(x) ≤ 0
Ta có bảng biến thiên:
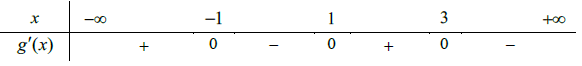
Vậy hàm số y = g(x) = f (x2 – 2x) có đúng 1 điểm cực tiểu là x = 1.
Ví dụ 5. Cho hàm số bậc bốn y = f(x). Bảng xét dấu bên dưới là của đạo hàm f’(x). Hàm số  có bao nhiêu điểm cực trị?
có bao nhiêu điểm cực trị?
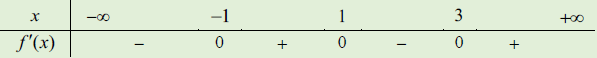
A .1
B. 2
C. 3
D. 4
Lời giải:
Chọn C
Ta có
g’(x) = 0
Bảng xét dấu:

Từ bảng xét dấu ta suy ra hàm số
có 3 điểm cực trị.
Lưu ý: Để xét dấu g’(x) , ta chọn một giá trị x0 thuộc khoảng đang xét rồi thay vào lần lượt các hàm x + 1,
để xét dấu chúng. Sau cùng sẽ suy ra dấu của g’(x) là tích của hai hàm trên. Chẳng hạn:
– Để xét dấu g’(x) trên khoảng
ta chọn giá trị x0 = 2 ∈ , thay số 2 vào x + 1, ta được dấu dương (+), thay 2 vào
ta được
> 3 nên
mang dấu dương (+) (xem bảng biến thiên ban đầu). Vì vậy mà dấu của g’(x) cũng là dấu dương (+).
– Để xét dấu g’(x) trên khoảng
, ta chọn giá trị x0 = 1 ∈ , thay số 1 vào x + 1 ta được dấu dương (+), thay số 1 vào
ta được
∈ (1;3) do đó
mang dấu âm (–) (xem bảng biến thiên ban đầu). Vì vậy mà dấu của g’(x) là dấu âm (–). Bằng cách thức này, ta có thể xét dấu g’(x) trên các khoảng còn lại và có được bảng xét dấu như lời giải trên.
Ví dụ 6. Cho hàm số có đồ thị như hình vẽ bên. Số điểm cực trị của hàm số đã cho là:

A. 3
B. 1
C. 2
D. 0
Lời giải
Chọn A
Hàm số có ba điểm cực trị.
Ví dụ 7. Cho hàm số y = f(x) có bảng biến thiên như sau

Tìm giá trị cực đại yCĐ và giá trị cực tiểu yCT của hàm số đã cho.
A. yCĐ = 2 và yCT = 0
B. yCĐ = 3 và yCT = 0
C. yCĐ = 3 và yCT = -2
D. yCĐ = -2 và yCT = 2
Lời giải
Chọn B
Dựa vào bảng biến thiên của hàm số ta có yCĐ = 3 và yCT = 0
Ví dụ 8. Cho hàm số f(x) có bảng biến thiên như sau:

Hàm số đạt cực đại tại:
A. x = -2
B. x = 3
C. x = 1
D. x = 2
Lời giải
Chọn C
Hàm số f(x) xác định tại x = 1, f’(1) = 0 và đạo hàm đổi dấu từ (+) sang (–).
Ví dụ 9. Cho hàm số y = ax4 + bx2 + c (a, b, c ∈ ℝ) có đồ thị như hình vẽ bên.

Số điểm cực trị của hàm số đã cho là
A. 3
B. 0
C. 1
D. 2
Lời giải
Chọn A
Dạng 3: Tìm tham số thỏa mãn điều kiện cực trị của hàm số
Ta có: y = ax3 + bx2 + cx + d (*)
⟶ y’ = 3ax2 + 2bx + c
Phương pháp:
Điều kiện để hàm số có n cực trị hoặc không có cực trị.
Ta xét bảng sau (a và ∆ là của đạo hàm y’):

Từ bảng trên, ta khẳng định:
– Hàm số (*) có hai cực trị
. Ta có thể thay ∆ > 0 bởi ∆’ > 0.
– Hàm số (*) có một cực trị
– Hàm số (*) có cực trị
– Hàm số (*) không có cực trị
.
Điều kiện cực trị cơ bản:
– Hàm số có cực trị tại x = x0
Ta có: y’(x0) = 0. Sau khi tìm được m thì thay ngược trở lại để lập bảng biến thiên cho hàm số rồi kết luận nhận hay loại giá trị m này.
– Hàm số đạt cực đại tại x = x0 (hoặc hàm số đạt cực tiểu tại x = x0)
Ta có: y’(x0) = 0. Sau khi tìm được m thì thay ngược trở lại để lập bảng biến thiên cho hàm số rồi kết luận nhận hay loại giá trị m này (hoặc có thể thay m tìm được vào đạo hàm cấp hai để xét dấu xem có phù hợp không).
Đồ thị hàm số có điểm cực trị là M(x0; y0)
Ta có:
⟶ tìm được m. Thay m trở lại đạo hàm để kiểm tra đạo hàm có đổi dấu khi x đi qua x0 hay không.
Đồ thị hàm số có hai điểm cực trị là A(xA; yA), B(xB; yB)
Ta có:
⟶ tìm được m, n,…
Điều kiện cực trị liên quan đến các trục tọa độ:
Đồ thị hàm số có hai điểm cực trị nằm khác phía trục Oy
Đồ thị hàm số có hai điểm cực trị nằm cùng phía trục Oy
Để ý: Trong điều kiện trên, ta đã thay điều kiện
bởi ac < 0. Lý do là hai số trái dấu đồng nghĩa với tích và thương của chúng là một số âm. Một khi a, c trái dấu rồi thì điều kiện a ≠ 0, ∆ = b2 – 4ac > 0 luôn được thỏa mãn
Vì vậy
Ta có biến đổi tương đương sau đây (phù hợp trắc nghiệm):
– Đồ thị hàm số có hai điểm cực trị nằm khác phía trục Ox
– Đồ thị hàm số có hai điểm cực trị nằm cùng phía trục Ox
(trong hai điều kiện trên thì y1, y2 là hai giá trị cực trị của hàm số bậc ba).
– Đồ thị hàm số có hai điểm cực trị cách đều trục Ox
– Đồ thị hàm số có hai điểm cực trị cách đều trục Oy
(I là điểm uốn)
Lưu ý: Cách tìm điểm uốn I đồ thị bậc ba y = ax3 + bx2 + cx + d = 0 là: y’ = 3ax2 + 2bx + c, y’’ = 6ax + 2b
, thay vào hàm số ban đầu để tìm yI ⇒ I(xI; yI).
Các công thức giải tích liên quan:
a) Định lí Vi-ét: Cho phương trình ax2 + bx + c = 0 (*) có hai nghiệm x1, x2
Ta có:
b) Công thức nghiệm của phương trình ax2 + bx + c = 0 (*)
(*) có hai nghiệm phân biệt
(*) có hai nghiệm trái dấu ⇔ ac < 0
(*) có hai nghiệm dương phân biệt
(*) có hai nghiệm âm phân biệt
.
c) Công thức hình học giải tích trong mặt phẳng:
Nếu △ABC có
thì
△ABC ⊥ tại A H52 ⇔ b1c1 + b2c2 = 0
Khoảng cách từ điểm M (xM ; yM ) đến ∆: ax + by + c = 0 là
Đặc biệt: d(M; Ox) = |yM|, d(M; Oy) = |xM|
Ví dụ 1. Với giá trị nào của m thì đồ thị hàm số y = ⅓x3 + mx2 + (m + 6) x – 2m + 1 có cực đại, cực tiểu.
A. m ∈ (-∞; -3) ∪ (2; +∞)
B. m ∈ (-∞; -3) ∪ (-2; +∞)
C. m ∈ (-∞; -2) ∪ 3; +∞)
D. m ∈ (-∞; 2) ∪ (3; +∞)
Lời giải:
Chọn C
Tập xác định : D = ℝ
Đạo hàm: y’ = x2 + 2mx + m + 6
Ta thấy a = 1 ≠ 0. Hàm số có cực đại, cực tiểu ⇔ y’ đổi dấu hai lần trên tập xác định
⇔ ∆’ > 0 ⇔ m2 – (m + 6) > 0
Ví dụ 2. Tìm tất các giá trị thực của tham số m để hàm số y = (m + 2) x3 + 3x2 + mx – 6 có 2 cực trị ?
A. m ∈ (-3;1) {2}
B. m ∈ (-3;1)
C. m ∈ (-∞;-3) ∪ (1; +∞)
D. m ∈ [-3;1]
Lời giải:
Chọn A
Tập xác định : D = ℝ
Đạo hàm: y’ = 3(m + 2) x2 + 6x + m
Hàm số có hai cực trị
Ví dụ 3. Tập hợp tất cả giá trị của m để hàm số y = = ⅓(m – 1) x3 – mx2 + mx – 5 có cực trị là:
A.
B. m ≠ 1
C. m > 0
D. m ≥ 0
Lời giải:
Chọn C
Tập xác định : D = ℝ
Đạo hàm: y’ = (m – 1) x2 – 2mx + m
Hàm số đã cho có cực trị khi và chỉ khi
Ví dụ 4. Tìm tất cả các giá trị thực của m để hàm số y = x3 – 2x2 + (m + 3) x – 1 không có cực trị?
A.
B.
C.
D.
Lời giải:
Chọn A
Tập xác định : D = ℝ
Đạo hàm: y’ = 3x2 – 4x + m + 3
Ta thấy a = 1 ≠ 0. Vậy hàm số không có cực trị ⇔ ∆’ ≤ 0
⇔ (-2)2 – 3(m + 3) ≤ 0 ⇔ -3m – 5 ≤ 0 ⇔
Ví dụ 5. Giá trị của m để hàm số y = x3 – 3mx2 + 3(m2 – 1) x + m đạt cực đại tại x = 1 là
A. m = -1
B. m = -2
C. m = 2
D. m = 0
Lời giải
Chọn C
Tập xác định: D = ℝ
Đạo hàm: y’ = 3x2 – 6mx + 3(m2 – 1)
Hàm số có cực đại tại x = 1 nên y’(1) = 0 ⇒ 3 – 6m + 3(m2 – 1) = 0 ⇒
Xét m = 0. Ta có y’ = 3x2 – 3; y’’ = 6x. Khi đó y’’(1) = 6 > 0 suy ra hàm số đạt cực tiểu tại x = 1 (loại m = 0 vì trái giả thiết).
Xét m = 2. Ta có y’ = 3x2 – 12x + 9; y’’ = 6x – 12. Khi đó y’’(1) = -6 < 0. Do đó hàm số đã cho đạt cực đại tại x = 1.
Vậy m = 2 thỏa mãn đề bài.
Ví dụ 6. Tìm tất cả các giá trị thực của tham số m để hàm số y = mx3 + x2 + (m2 – 6) x + 1 đạt cực tiểu tại x = 1
A.
B. m = 1
C. m = -4
D. m > – ⅓
Lời giải:
Tập xác định : D = ℝ
Đạo hàm: y’ = 3mx2 + 2x + m2 – 6
Hàm số đạt cực tiểu tại x = 1 ⇒ y’(1) = 0 ⇒ 3m+ 2 + m2 – 6 = 0 ⇒
Xét m = 1. Ta có y’ = 3x2 + 2x – 5; y’’ = 6x + 2. Khi đó y’’(1) = 8 > 0, hàm số đã cho đạt cực tiểu tại x = 1. Vì vậy m = 1 thỏa mãn.
Xét m = -4. Ta có y’ = -12x2 + 2x + 10; y’’ = -24x + 2. Khi đó y’’(1) = -22 < 0, suy ra hàm số đạt cực đại tại x = 1. Điều này trái với giả thiết nên ta loại m = -4 .
Dạng 4: Bài toán tham số có liên quan đến đường thẳng đi qua hai điểm cực trị của đồ thị hàm số y = ax3 + bx2 + cx + d (*)
Viết phương trình đường thẳng qua hai điểm cực trị của đồ thị y = ax3 + bx2 + cx + d (*):
Giả sử đồ thị hàm số (*) có hai điểm cực trị, ta thực hiện theo những cách sau để viết phương trình đường thẳng qua hai điểm cực trị đó :
Phương pháp tự luận :
Chia f(x) cho f’(x) như sau:
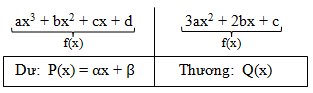
Khi đó, hàm số được viết lại: f(x) = f’(x)․Q(x) + αx + β
Tọa độ các điểm cực trị thỏa H64 hay f(x) = αx + β
Phương pháp Trắc nghiệm:
– Cách viết 1:
– Cách viết 2:
Tìm điểm uốn của đồ thị hàm số y = ax3 + bx2 + cx + d (*):
Xét hình dáng đồ thị hàm bậc ba bên dưới (đồ thị có hai điểm cực trị A, B), nhìn vào đồ thị tại lân cận điểm A, ta thấy bề lõm của nó hướng xuống (lồi); nhìn vào đồ thị tại lân cận điểm B, ta thấy bề lõm của nó hướng lên trên (lõm). Vậy sẽ có một ranh giới để đồ thị chuyển từ lồi sang lõm, ranh giới ấy được gọi là điểm uốn của đồ thị (trong hình là điểm I).
– Đặc biệt: Nếu đồ thị hàm số có hai điểm cực trị là A, B thì I sẽ là trung điểm của đoạn AB.
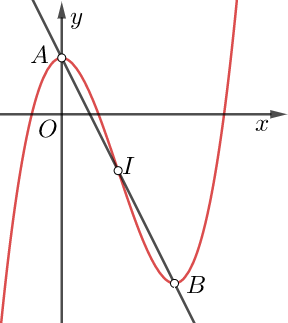
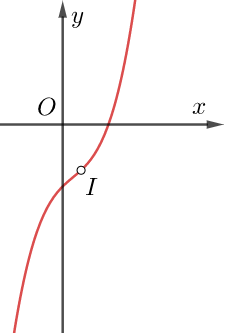
Cách tìm điểm uốn I:
– Bước 1: Tính y’ = 3ax2 + 2bx + c, y’’ = 6ax + 2b
– Bước 2: Cho y’’ = 6ax + 2b = 0
, thay vào hàm số để yI . Từ đây ta có điểm uốn I(xI; yI) của đồ thị hàm bậc ba.
Tính chất quan trọng: Điểm uốn I chính là tâm đối xứng của đồ thị hàm bậc ba tức là bất kỳ đường thẳng nào qua I nếu cắt đồ thị tại hai điểm còn lại M, N thì I luôn là trung điểm đoạn MN.
Ví dụ 1. Cho hàm số y = f(x) = x3 – x + m (1). Viết phương trình đường thẳng đi qua hai điểm cực trị của đồ thị hàm số (1).
A.
B. y = -x – m
C.
D.
Đánh giá :
Với bài toán này, xin được hướng dẫn hai cách để bạn đọc lựa chọn phương án tối ưu cho mình.
– Cách giải 1: Làm theo lý luận truyền thống.
– Cách giải 2: Dựa vào công thức đã cung cấp.
Với cách giải 1, ta thực hiện phép chia y cho y’ trong giấy nháp như sau :

Lời giải:
Cách giải 1:
Chọn D
Tập xác định : D = ℝ
Đạo hàm: y’ = 3x2 – 1; y’ = 0
nên hàm số luôn có 2 cực trị.
Hàm số được viết lại
Tọa độ các điểm cực trị của đồ thị hàm số luôn thỏa mãn:
Phương trình đường thẳng qua hai điểm cực trị của đồ thị là
Cách giải 2:
Tập xác định: D = ℝ
Đạo hàm: y’ = 3x2 – 1; y’ = 0
nên hàm số luôn có 2 cực trị.
Dựa vào công thức
, ta viết phương trình đường thẳng qua hai điểm cực trị như sau:
Ví dụ 2. Cho biết có một tham số m để đồ thị hàm số y = 2x3 + 3(m – 3) x2 + 11 – 3m có hai điểm cực trị, đồng thời hai điểm cực trị đó và điểm C(0; -1) thẳng hàng. Tìm khẳng định đúng:
A. m ∈ (3; 6)
B. m ∈ (4; 7)
C. m ∈ (1; 4)
D. m ∈ (-1; 2)
Lời giải:
Chọn A
Cách giải 1: Chia y cho y’ như sau:

Tập xác định: D = ℝ
Đạo hàm: y’ = 6x2 + 6(m – 3) x
y’ = 0 ⇔ 6x(x + m – 3) = 0 ⇔
Hàm số có hai cực trị ⇔ 3 – m ≠ 0 ⇔ m ≠ 3
Tọa độ các điểm cực trị của đồ thị hàm số luôn thỏa mãn :
⇔ y = -(m – 3)2 x + 11 – 3m
Điểm C(0; -1) thuộc đường thẳng qua hai điểm cực trị nên -1 = 11 – 3m ⇔ m = 4 (thỏa mãn).
Cách giải 2:
Tập xác định: D = ℝ
Đạo hàm: y’ = 6x2 + 6(m – 3) x
y’ = 0 ⇔ 6x(x + m – 3) = 0 ⇔
Hàm số có hai cực trị ⇔ 3 – m ≠ 0 ⇔ m ≠ 3
Áp dụng công thức, ta viết phương trình đường thẳng qua hai điểm cực trị của đồ thị :
⇔ y = 2x3 + 3(m – 3) x2 + 11 – 3m – [x2 + (m – 3) x](2x + m – 3)
⇔ y = 2x3 + 3(m – 3) x2 + 11 – 3m – [2x3 + 3(m – 3) x2 + (m – 3)2 x]
⇔ -(m – 3)2 x + 11 – 3m
Điểm C(0; -1) thuộc đường thẳng qua hai điểm cực trị nên -1 = 11 – 3m ⇔ m = 4 (thỏa mãn).
Ví dụ 3. Tìm giá trị của tham số m để đồ thị của hàm số y = x3 – 3x2 – mx + 2 có các điểm cực đại và cực tiểu cách đều đường thẳng y = x – 1.
A.
B. -3
C.
D. 0
Đánh giá : Phương trình y’ = 0 ⇔ 3x2 – 6x – m = 0 không thể cho ra nghiệm đẹp như ta muốn nên những bài toán liên quan tọa độ điểm cực trị đều cần đến phương trình đường thẳng đi qua hai điểm cực trị.
Lời giải:
Chọn D
Tập xác định : D = ℝ
Đạo hàm: y’ =3x2 – 6x – m
Hàm số có hai cực trị ⇔ ∆’ > 0 ⇔ 9 + 3m > 0 ⇔ m > -3 (*)
Phương trình đường thẳng qua hai điểm cực trị của đồ thị là ∆:
Các điểm cực trị cách đều đường thẳng d: y = x – 1
![]()
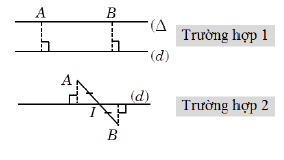
Trường hợp 1:
(loại do (*))
Trường hợp 2: Gọi hai điểm cực trị của đồ thị hàm số là
Điểm I là trung điểm của AB nên:
I ∈ d: y = x – 1 ⇔ -m = 1 – 1 ⇔ m = 0 (thỏa mãn do (*))
Dạng 5: Bài toán tìm tham số thỏa mãn điều kiện cực trị hàm số y = ax4 + bx2 + c
Số cực trị của hàm số y = ax4 + bx2 + c
Đạo hàm: y’ = 4ax3 + 2bx = 2x (2ax2 + b); y’ = 0
Nhìn vào phương trình y’ = 0, ta thấy luôn có một nghiệm x = 0. Do đó việc biện luận tiếp theo sẽ phụ thuộc vào phương trình (*) . Từ (*) ta thấy:
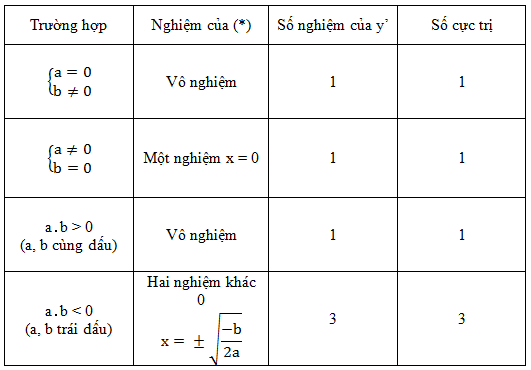
Từ đây, ta có thể khẳng định:
Hàm số không có cực trị ⇔ a = b = 0
Hàm số có cực trị ⇔ a2 + b2 > 0
Hàm số có một cực trị ⇔
Hàm số có ba cực trị ⇔ a․b < 0
Lưu ý : Việc sử dụng a2 + b2 > 0 là thể hiện a, b không đồng thời bằng 0, tuy nhiên BPT a2 + b2 > 0 mang tính phức tạp do bậc của m có thể ≥ 4. Để khắc phục điều này, ta dùng phương pháp phủ định như sau:
Xét
(Giải tìm) ⟶
Quay lại giải a2 + b2 > 0 tức là lấy phủ định kết quả của bước một. Ta có
Tìm điều kiện để hàm số y = ax4 + bx2 + c thỏa mãn điều kiện K:
– Bước 1: Tập xác định: D = ℝ. Đạo hàm: y’ = 4ax3 + 2bx = 2x (2ax2 + b)
y’ = 0 ⇔
– Bước 2: Điều kiện hàm số có một cực trị (hoặc có ba cực trị) – Xem mục 1 (lý thuyết).
– Bước 3: Dựa vào điều kiện K đề tìm tham số m rồi so sánh điều kiện có cực trị (bước 2) trước khi kết luận.
Xử lý điều kiện K (Công thức trắc nghiệm):
Hàm số có cực trị và thỏa mãn:
Hàm số có cực đại mà không có cực tiểu

Hàm số có cực tiểu mà không có cực đại
Ba cực trị tạo thành tam giác vuông hoặc đều, ta dùng công thức nhanh
Ba cực trị tạo thành tam giác vuông
Ba cực trị tạo thành tam giác đều
Ba cực trị tạo thành tam giác có diện tích S.
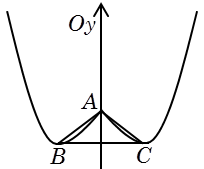
Ta dùng công thức nhanh bình phương diện tích:
Tọa độ ba điểm cực trị của đồ thị là A(0;c),
với ∆ = b2 – 4ac
Tam giác ABC có
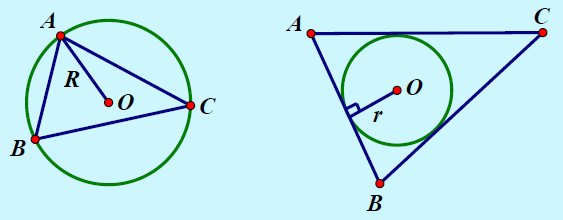
Công thức diện tích khác:
; S = pr .Trong đó:
R, r theo thứ tự là bán kính đường tròn ngoại tiếp và nội tiếp của tam giác
a, b, c là độ dài ba cạnh;
là nửa chu vi tam giác
Ví dụ 1. Có tất cả bao nhiêu giá trị nguyên của m trên miền [-10;10] để hàm số y = x4 – 2(2m + 1) x2 + 7 có ba điểm cực trị?
A. 20
B. 10
C. Vô số
D. 11.
Lời giải:
Chọn D
Cách 1: Tự luận
Tập xác định: D = ℝ .
Ta có y’ = 4x3 – 4(2m + 1) x
y’ = 0 ⇔ 4x3 – 4(2m + 1) x = 0
Hàm số đã cho có ba điểm cực trị khi và chỉ khi phương trình y’ = 0 có ba nghiệm phân biệt
⇔ Phương trình (*) có hai nghiệm phân biệt khác 0 ⇔ 2m + 1 > 0 ⇔ m > -½ .
Vì m nguyên thuộc [-10;10] nên m ∈ {0; 1; 2; 3; 4; 5; 6; 7; 8; 9; 10}
Cách 2: Trắc nghiệm
Hàm số có ba cực trị khi và chỉ khi a․b < 0 ⇔ 1․[-2(2m + 1)] < 0 ⇔ 2(2m + 1) > 0 ⇔ m > -½.
Ví dụ 2. Tìm tất cả giá trị của tham số m để hàm số y = mx4 + (m2 – 9) x2 + 10 có 3 cực trị.
A. m ∈ (0; 3)
B. m ∈ (3; +∞)
C. m ∈ (-∞; -3) ∪ (0; 3)
D. m ∈ (-3; 0) ∪ (3; +∞)
Lời giải:
Chọn C
Cách 1: Tự luận
Tập xác định: D = ℝ .
Ta có y’ = 4mx3 – 2(m2 – 9) x = 2x (2mx2 + m2 – 9)
y’ = 0 ⇔
Hàm số đã cho có 3 cực trị ⇔ y’ = 0 có 3 nghiệm phân biệt ⇔ Phương trình (1) có hai nghiệm phân biệt khác 0 .
Suy ra m ∈ (-∞; -3) ∪ (0; 3)
Cách 2: Trắc nghiệm
Hàm số có ba cực trị khi và chỉ khi ab < 0 ⇔ m (m2 – 9) < 0
Ví dụ 3. Tìm tất cả các giá trị của tham số m để đồ thị hàm số y = mx4 + (m – 1) x2 + 1 – 2m chỉ có một cực trị.
A. m ≥ 1
B. m ≤ 0
C. 0 ≤ m ≤ 1
D. m ≤ 0 hoặc m ≥ 1
Lời giải:
Chọn D
Hàm số có một cực trị khi và chỉ khi
⇔ m ≤ 0 ∨ m ≥ 1
Vậy m m ≤ 0 hoặc m ≥ 1 thỏa mãn đề bài
Ví dụ 4. Tìm tất cả các giá trị của tham số m để hàm số  có cực tiểu mà không có cực đại.
có cực tiểu mà không có cực đại.
A. m ≥ 0
B. m ≤ 0
C. m ≥ 1
D. m = -1
Nhận xét : Có hai trường hợp để hàm số y = ax4 + bx2 + c có cực tiểu mà không có cực đại:
Một là: Hàm bậc bốn có đúng một cực trị và là cực tiểu, khi đó:
Hai là: Hàm số trở thành hàm bậc hai (đồ thị parabol có bề lõm hướng lên), ta có:
Lời giải :
Chọn B
Ta thấy
, vì vậy điều kiện bài toán tương đương với b ≥ 0 ⇔ -2m ≥ 0 ⇔ m ≤ 0
Vậy m ≤ 0 thỏa mãn đề bài.
Ví dụ 5. Tìm tất cả các giá trị của m để hàm số y = (m2 – 1) x4 + mx2 + m – 2 chỉ có một điểm cực đại mà không có điểm cực tiểu.
A. -1,5 < m ≤ 0
B. m ≤ -1
C. -1 ≤ m ≤ 0
D. -1 < m < 0,5
Lời giải:
Chọn C
Hàm số có một điểm cực đại mà không có cực tiểu
Giải (1):
Giải (2):
Từ (*) và (**) suy ra -1 ≤ m ≤ 0
Dạng 6: Tìm tham số thỏa mãn điều kiện cực trị của những hàm số khác.
Hàm số phân thức bậc hai trên bậc một
Tập xác định: D = ℝ
Đạo hàm:
với
Hàm số có hai điểm cực trị ⇔ y’ đổi dấu hai lần trên tập xác định ⇔ g(x) = 0 có hai nghiệm phân biệt khác
.
Đường thẳng đi qua hai điểm cực trị của đồ thị có phương trình:
Hàm số chứa dấu giá trị tuyệt đối:
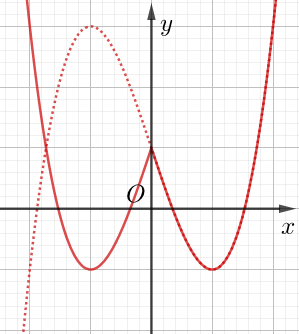
Hàm số y = |f(x)|
Đạo hàm:
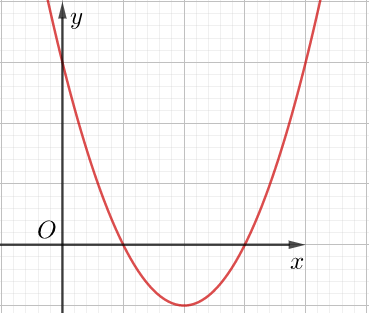
Cho trước đồ thị hàm số y = f(x) liên tục trên D. Ta xác định đồ thị hàm y = |f(x)|:
– Bước 1: Giữ nguyên phần đồ thị y = f(x) nằm phía trên trục hoành.
– Bước 2: Lấy đối xứng phần đồ thị y = f(x) nằm dưới trục hoành qua trục hoành.
Hợp của hai phần trên (bỏ phần dưới trục hoành), ta được đồ thị hàm y = |f(x)|.
Minh họa:
Đồ thị y = f(x)
Đồ thị y = |f(x)|
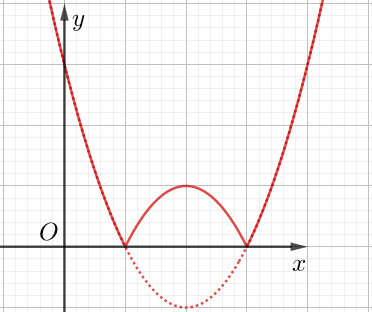
Đúc kết :
Số cực trị hàm y = |f(x)| = số cực trị hàm y = f(x) + Số giao điểm (không tính tiếp xúc)
Hàm số y = f(|x|):
Cho trước đồ thị hàm số y = f(x) liên tục trên D. Ta xác định đồ thị hàm y = f(|x|)
– Bước 1: Giữ nguyên phần đồ thị y = f(x) nằm bên phải trục tung (ứng với x ≥ 0); bỏ đi phần đồ thị y = f(x) nằm bên trái trục tung (ứng với x < 0)
– Bước 2: Lấy đối xứng phần đồ thị y = f(x) nằm bên phải trục tung qua trục tung.
Hợp của hai phần trên, ta được đồ thị hàm y = f(|x|)
Minh họa:
Đồ thị y = f(x)
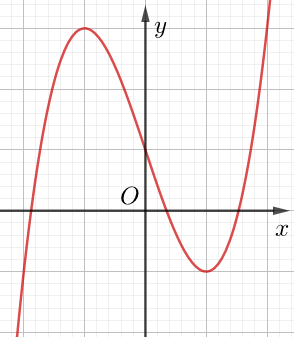
Đồ thị y = f(|x|)
Đúc kết :
Xét hàm đa thức f(x) có tập xác định là ℝ (chắc chắn đồ thị hàm này sẽ cắt Oy tại một điểm), ta có:
Số cực trị hàm y = f(|x|) = 2 × Số cực trị nằm bên phải Oy của hàm y = f(x) +1
Để cho dễ nhớ, ta gọi n là số cực trị dương của hàm số y = f(x), khi ấy số cực trị của hàm số y = f(|x|) bằng 2n + 1.
Ví dụ 1. Tìm tất cả giá trị tham số m sao cho hàm số  có cực đại, cực tiểu.
có cực đại, cực tiểu.
A. m ∈ ℝ
B. m = 0
C. m = 1
D. m = -1
Lời giải:
Chọn A
Tập xác định: D = ℝ {m}.
Đạo hàm:
Hàm số có cực đại, cực tiểu ⇔ y’ đổi dấu hai lần trên tập xác định ⇔ g(x) = 0 có hai nghiệm phân biệt khác m
Ví dụ 2. Tìm tất cả giá trị tham số m để điểm A(1; -3) cùng với hai điểm cực trị của đồ thị hàm số  tạo thành ba điểm không thẳng hàng.
tạo thành ba điểm không thẳng hàng.
A.
B. m ≠ 1
C.
D.
Lời giải:
Chọn C
Tập xác định: D = ℝ {-1}.
Đạo hàm:
Hàm số có hai cực trị ⇔ y’ đổi dấu hai lần trên tập xác định ⇔ g(x) = 0 có hai nghiệm phân biệt khác -1
Phương trình đường thẳng qua hai điểm cực trị của đồ thị là d:
Điểm A(1; -3) ∉ d ⇔ -3 ≠ 2․1 + 2m ⇔
Vậy m < 1 và
thỏa mãn đề bài.
Ví dụ 3. Cho hàm số  (m là tham số). Tìm tất cả các giá trị của tham số m để hàm số có giá trị cực đại là 7.
(m là tham số). Tìm tất cả các giá trị của tham số m để hàm số có giá trị cực đại là 7.
A. m = 7
B. m = 5
C. m = -9
D. m = -5
Lời giải:
Chọn C
Điều kiện x ≠ m.
Đạo hàm:
y’ = 0
Vì 1 – m ≠ -1 – m, ∀ m ∈ ℝ nên hàm số luôn có hai điểm cực trị ∀ m ∈ ℝ.
Phương trình đường thẳng qua hai điểm cực trị của đồ thị là y = 2x + m
Suy ra y (1 – m) = 2 – m, y (-1 – m) = -2 – m
Ta có bảng biến thiên:
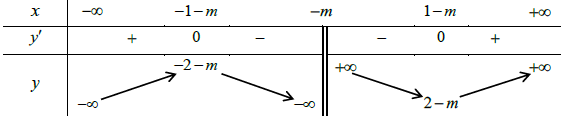
Ta có yCĐ = -2 – m = 7 ⇔ m = -9
Tài liệu về cực trị hàm số
#1. Bài tập cực trị của hàm số
| Thông tin tài liệu | |
| Tác giả | Thầy Diệp Tuân |
| Số trang | 126 |
| Lời giải chi tiết | Không |
Mục lục tài liệu
- Lý thuyết cực trị của hàm số
- Dạng 1: Tìm các điểm cực trị của hàm số.
- Dạng 2: Định tham số m để hàm số f (x) đạt cực trị.
- Dạng 3: Ứng dụng cực trị giải phương trình, bất phương trình, hệ phương trình đại số.
- Dạng 4: Xác định cực trị của hàm hợp khi biết đồ thị, BBT của hàm số con
- Dạng 5: Cực trị của hàm giá trị tuyệt đối
→ TẢI ĐẦY ĐỦ TÀI LIỆU XUỐNG


#2. Bài tập cực trị hàm số Vận Dụng Cao
| Thông tin tài liệu | |
| Số trang | 72 |
| Lời giải chi tiết | Có |
Mục lục tài liệu:
– Kiến thức cơ bản cần nắm
– Dạng 1: Cho hàm số f (x) hoặc f ‘(x) . Tìm điểm cực trị, giá trị cực trị
– Dạng 2. Tìm (điểm) cực trị thông qua bảng xét dấu, bảng biến thiên của đạo hàm
– Dạng 3. Tìm (điểm) cực trị thông qua đồ thị f , f’ , f’’
– Dạng 4: Cực trị hàm bậc ba
– Dạng 5. Cực trị hàm bậc bốn trùng phương
– Dạng 6. Cực trị hàm phân thức
– Dạng 7: Cực trị của hàm chứa căn
– Dạng 8: Cực trị của hàm bậc cao và hàm lượng giác
– Dạng 9:Tìm cực trị của hàm số chứa trị tuyệt đối
– Dạng 10: Tìm cực trị của hàm số trị tuyệt đối nếu biết bảng biến thiên hoặc đồ thị
– Dạng 11: Một số bài toán sử dụng phép dịch chuyển đồ thị
– Dạng 12: Định tham số để hàm số chứa dấu trị tuyệt đối có n điểm cực trị
– Dạng 13: Cho bảng biến thiên, định giá trị tham số để hàm số trị tuyệt đối có n điểm cực trị
– Dạng 14: Cho đồ thị, định tham số để có hàm số có n điểm cực trị
– Dạng 15. Biết được đồ thị của hàm số f (x) tìm (số điểm) cực trị của hàm ẩn
– Dạng 16. Tìm (số điểm) cực trị hàm ẩn biết đồ thị của hàm số f ‘(x)
– Dạng 17. Biết được f ‘(x) hoặc bảng xét dấu, bảng biến thiên của f ‘(x), tìm số điểm cực trị của hàm ẩn
→ TẢI ĐẦY ĐỦ TÀI LIỆU XUỐNG




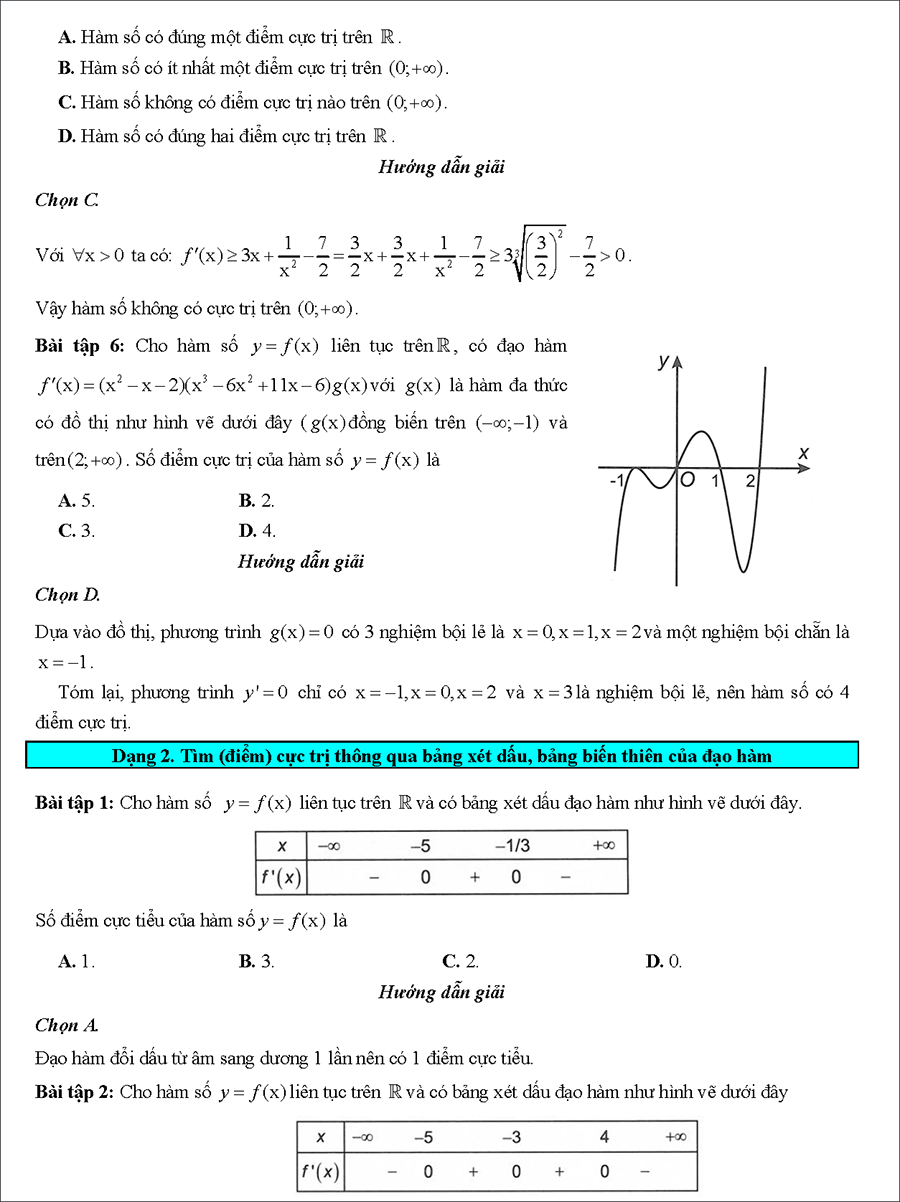
#3. Bài tập cực trị của hàm số Vận Dụng và Vận Dụng Cao
| Thông tin tài liệu | |
| Tác giả | Giáo viên THPT Đầm Dơi |
| Sô trang | 115 |
| Lời giải chi tiết | Có |
Mục lục tài liệu:
– Dạng 1: Tìm cực trị của hàm số
– Dạng 2: Cực trị hàm bậc ba, hàm trùng phương
– Dạng 3: Cực trị các hàm số khác
→ TẢI ĐẦY ĐỦ TÀI LIỆU XUỐNG


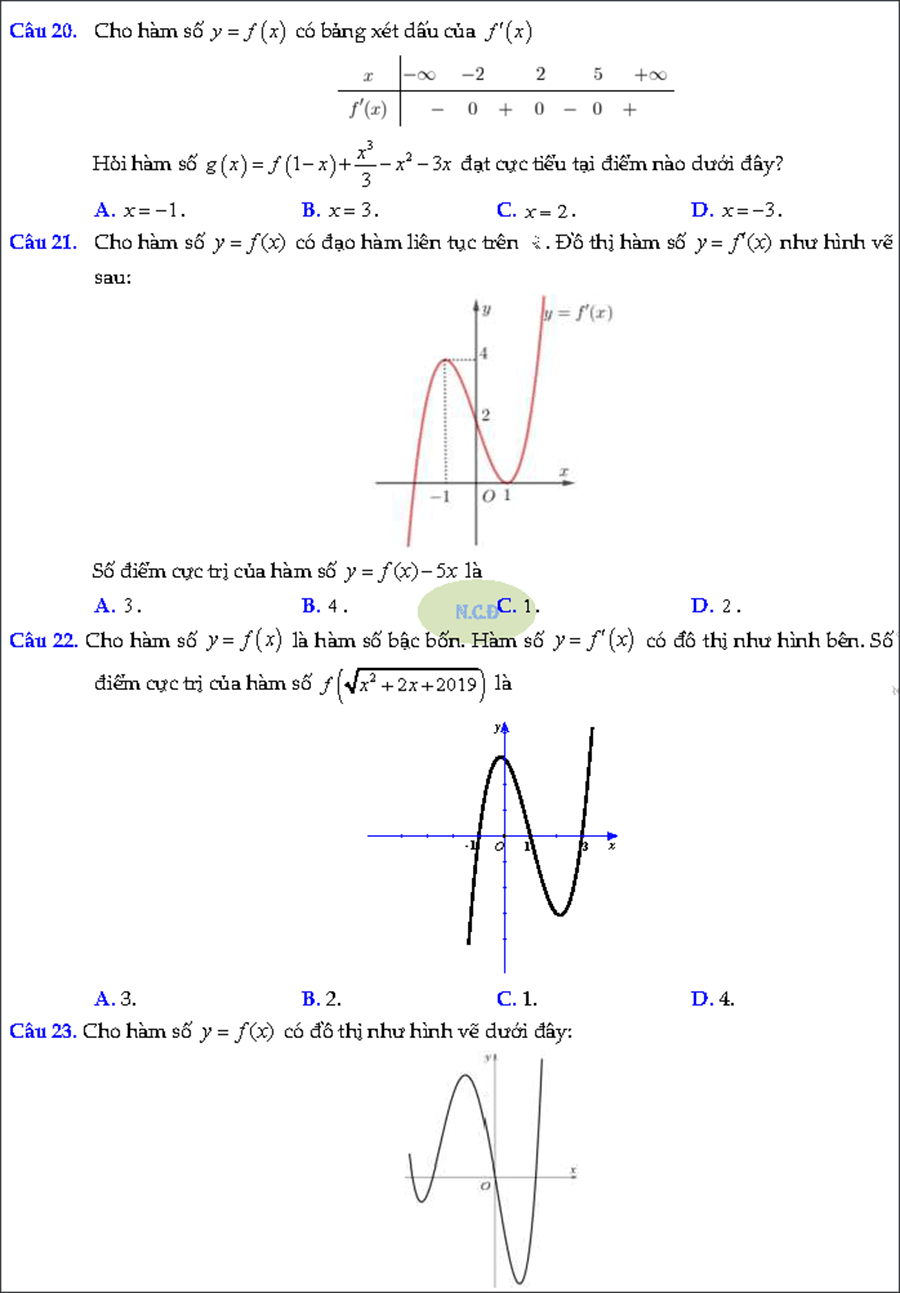
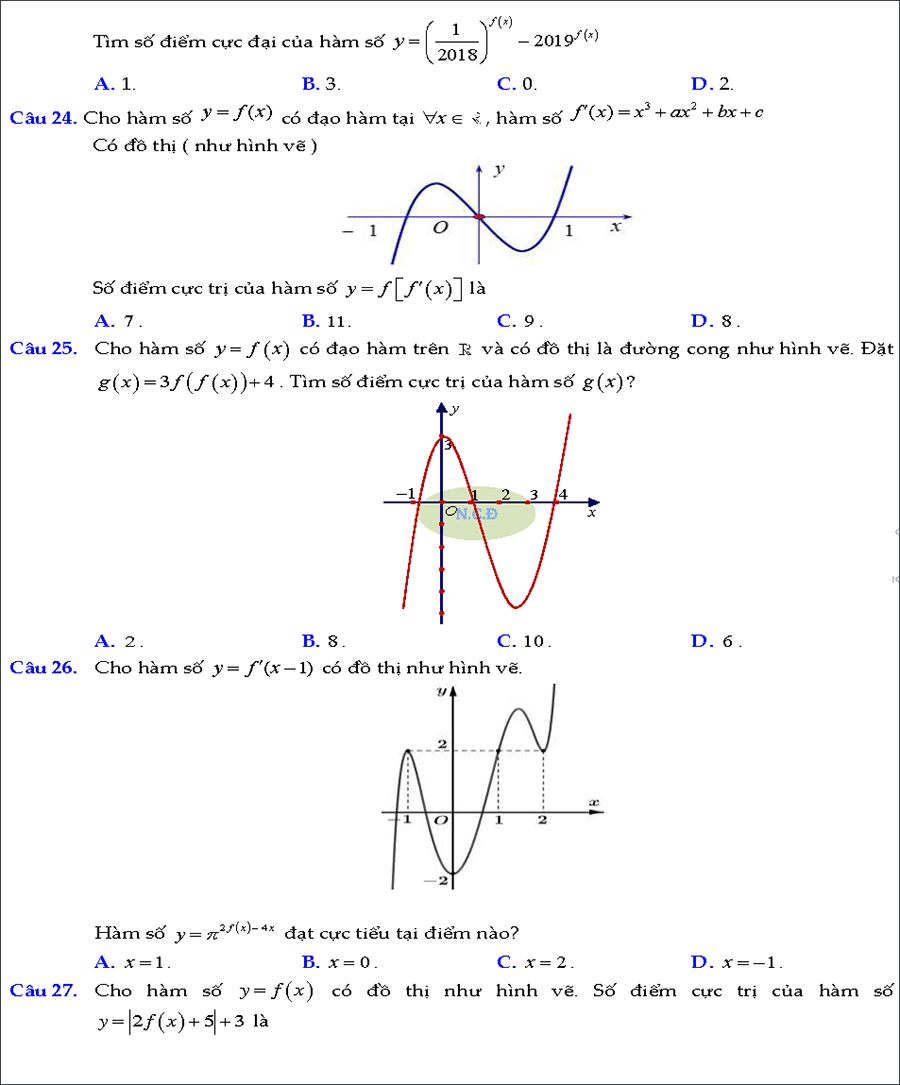
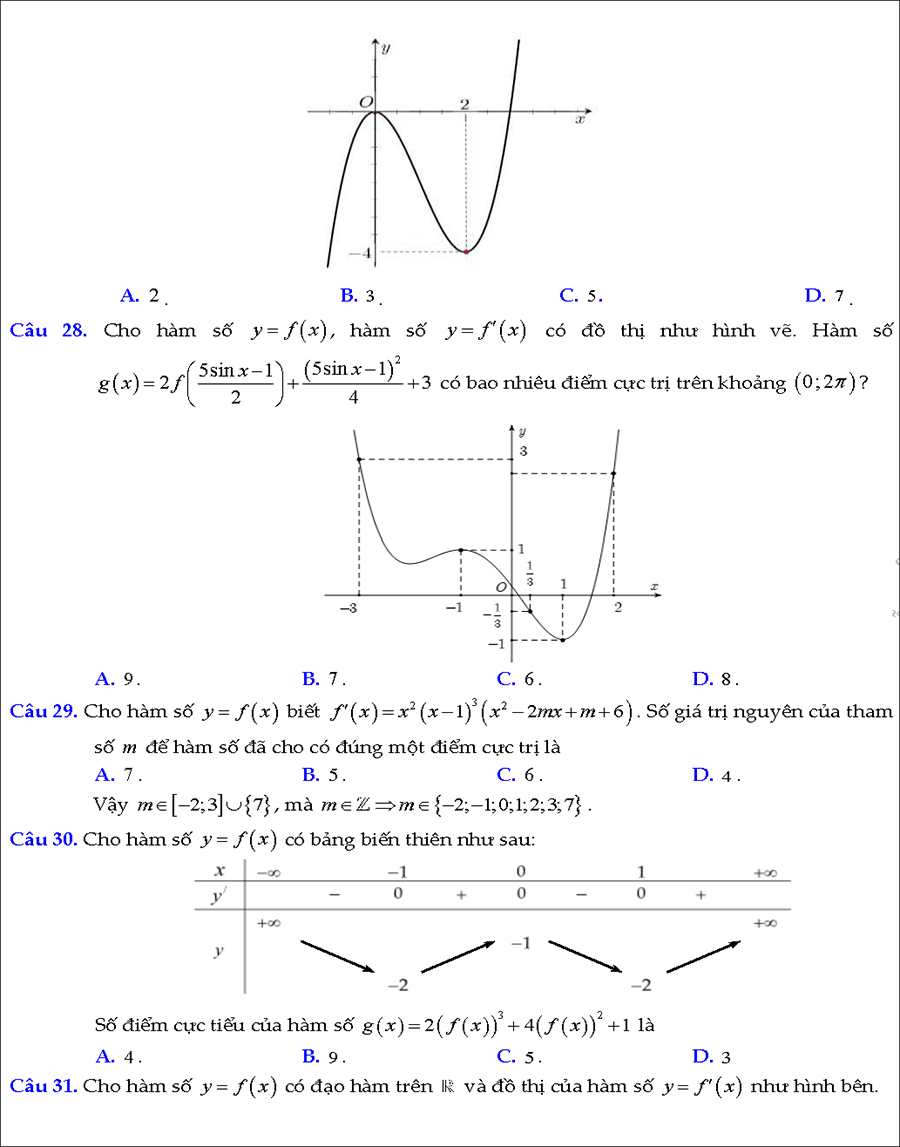
#4. Cực trị của hàm ẩn
| Thông tin tài liệu | |
| Tác giả | Thầy Nguyễn Minh Nhiên |
| Số trang | 17 |
| Lời giải chi tiết | Có |
Các bài toán về xác định cực trị của hàm số cho bởi bảng biến thiên, đồ thị hay đạo hàm của nó (ta vẫn gọi là cực trị hàm ẩn) thường gây khó khăn cho nhiều thí sinh. Tài liệu này sẽ giúp các em có tìm ra hướng tiếp cận đơn giản nhất để giải quyết các bài toán đó thật dễ dàng.
→ TẢI ĐẦY ĐỦ TÀI LIỆU XUỐNG



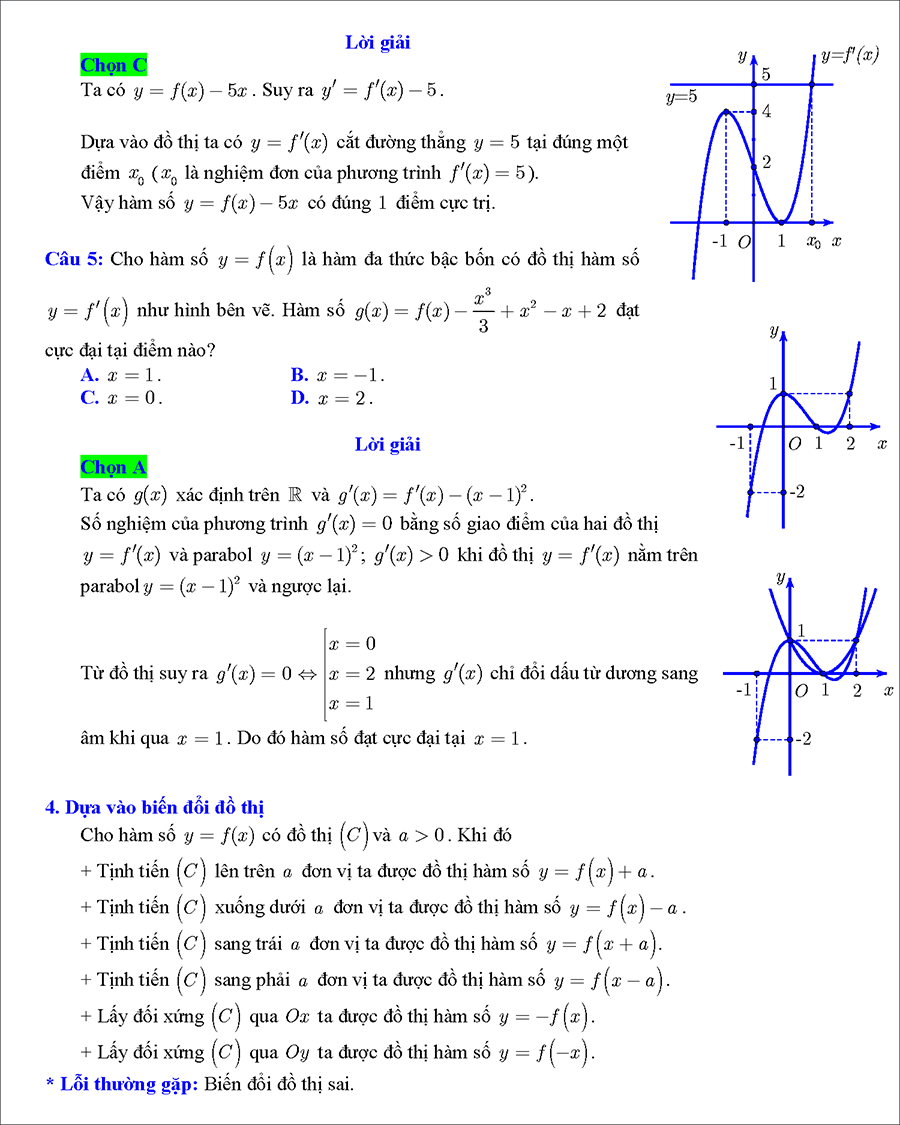
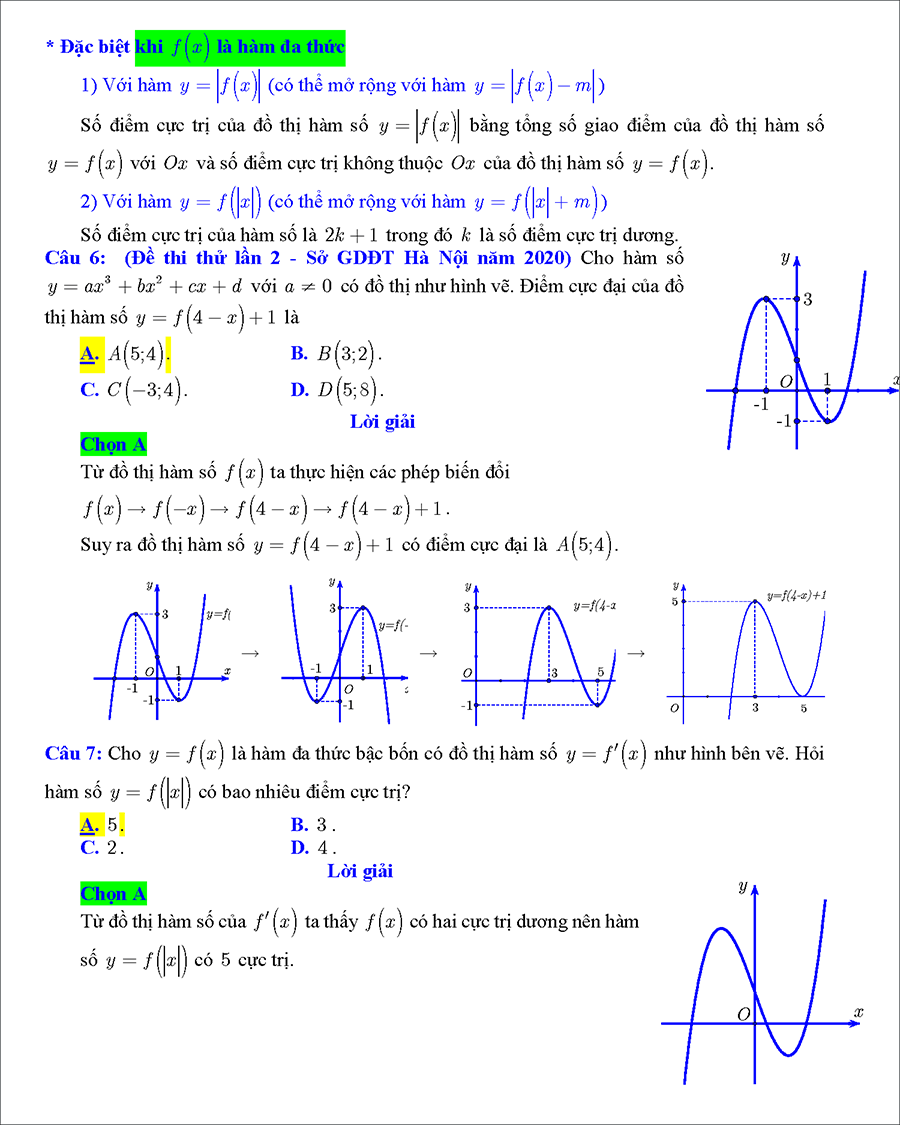
#5. Cực trị hàm hợp và hàm liên kết (vận dụng cao)
| Thông tin tài liệu | |
| Tác giả | Thầy Đặng Việt Đông |
| Số trang | 78 |
| Lời giải chi tiết | Có |
Mục lục tài liệu:
– Dạng 1: Cực trị f(x), f(u),… biết các đồ thị không tham số
– Dạng 2: Cực trị f(x), f(u),… biết các BBT, B XD không tham số
– Dạng 3: Cực trị f(x), f(u),…liên quan biểu t hức đạo hàm không tham số )
– Dạng 4: Cực trị của hàm liên kết h(x) = f(u) + g(x) biết các BBT, đồ thị không tham số
– Dạng 5: Cực trị hàm hợp f(u), g(f(x)), hàm liên kết…có tham số.
→ TẢI ĐẦY ĐỦ TÀI LIỆU XUỐNG
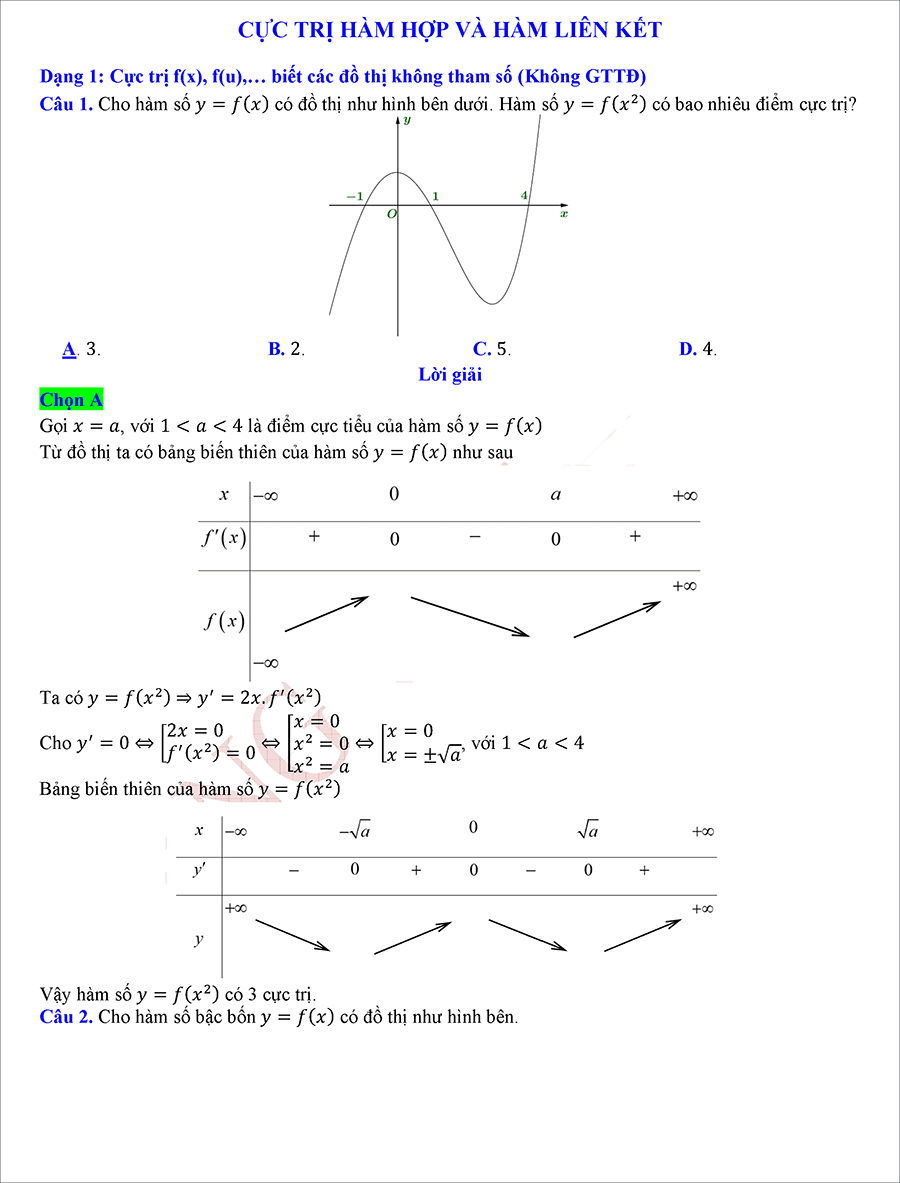
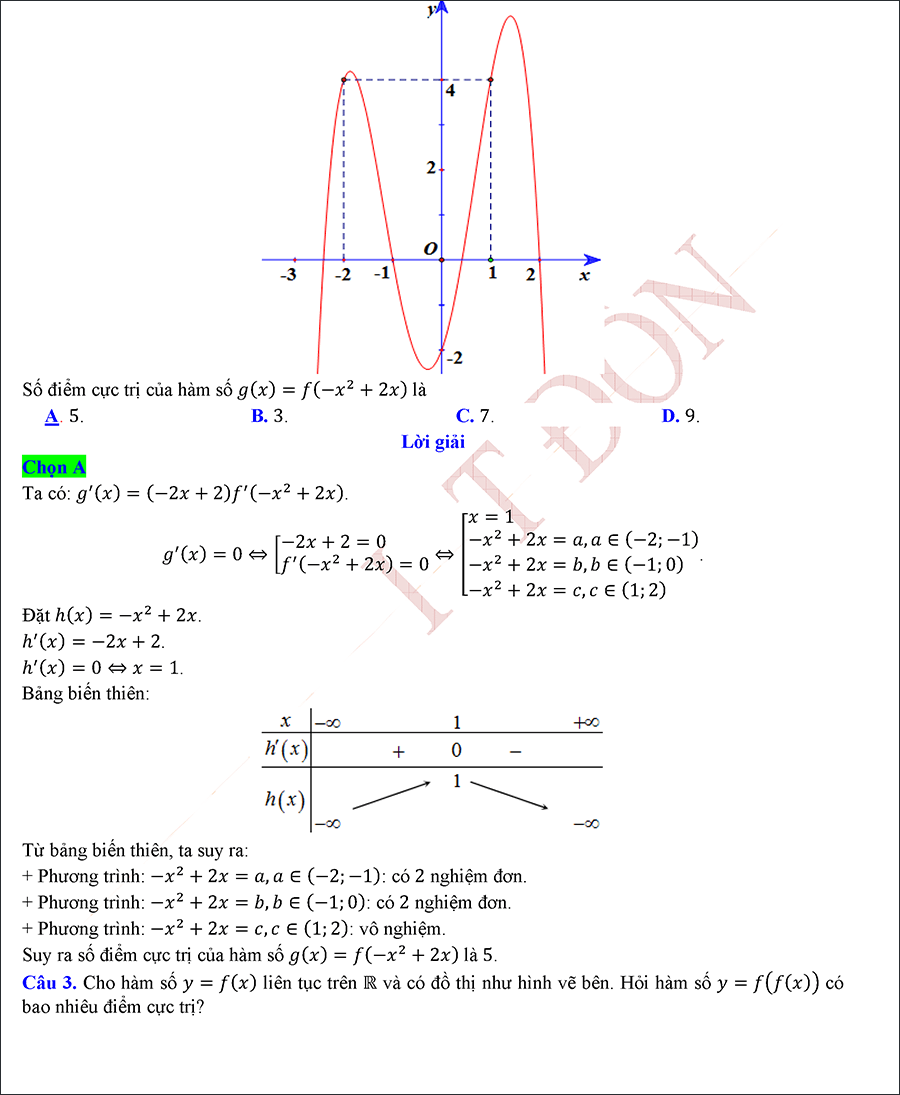
#6. Cực trị hàm số chứa giá trị tuyệt đối
| Thông tin tài liệu | |
| Số trang | 44 |
| Lời giải chi tiết | Có |
Mục lục tài liệu:
– Dạng 1: Cực trị hàm số chứa dấu giá trị tuyệt đối khi cho hàm số y = f’(x).
– Dạng 2: Cực trị hàm số chứa dấu giá trị tuyệt đối khi cho bảng biến thiên và bảng xét dấu.
– Dạng 3: Cực trị hàm số chứa dấu giá trị tuyệt đối khi cho đồ thị.
– Dạng 4: Cực trị hàm số chứa dấu giá trị tuyệt đối của hàm đa thức chứa tham số.
→ TẢI ĐẦY ĐỦ TÀI LIỆU XUỐNG


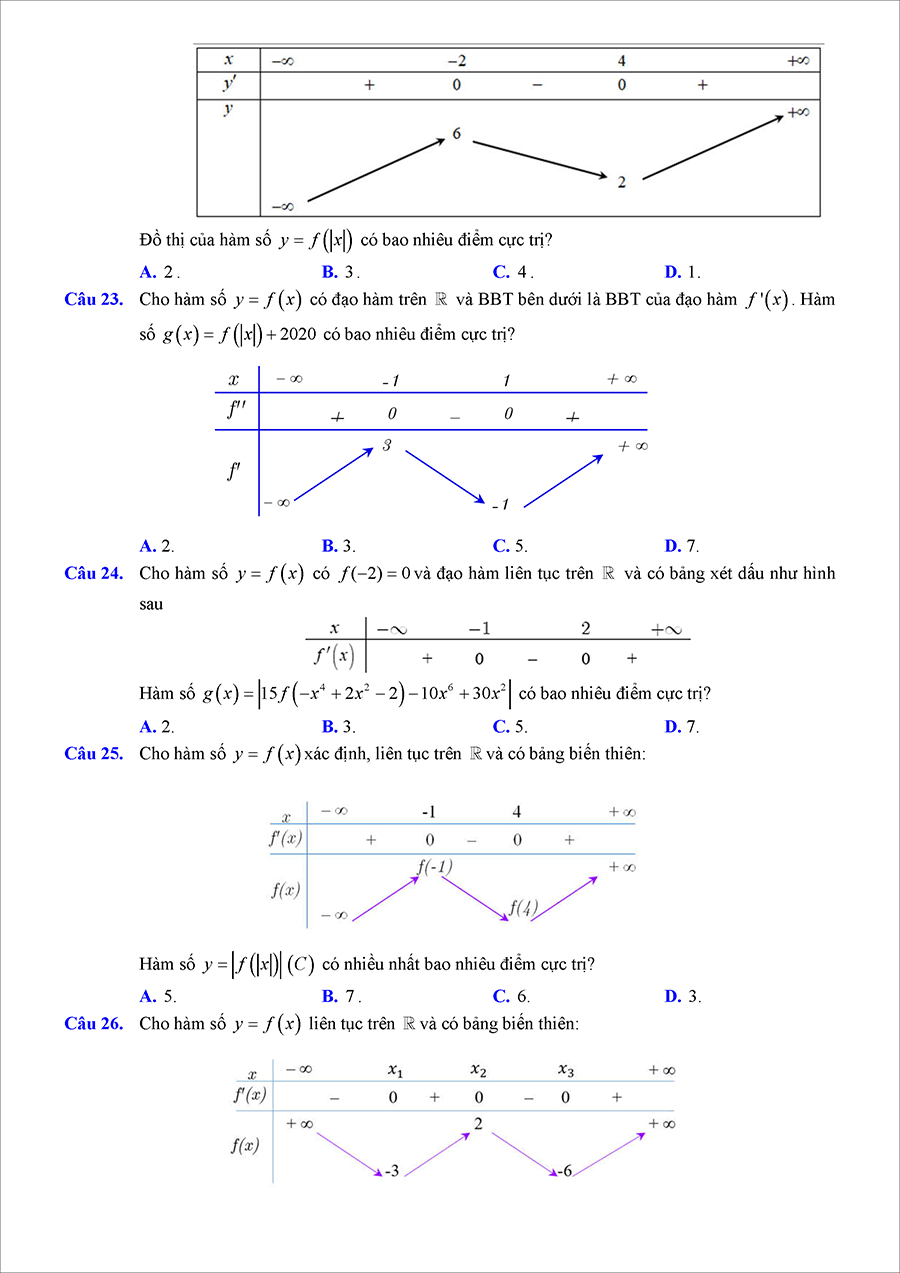

#7. Cực trị hình học
| Thông tin tài liệu | |
| Tác giả | Cô Nguyễn Thị Thúy Hằng |
| Số trang | 75 |
| Lời giải chi tiết | Có |
Mục lục tài liệu:
– Giải toán cực trị hình học bằng hình học thuần túy.
– Giải toán cực trị hình học bằng công cụ đại số.
– Giải toán cực trị hình học bằng các phương pháp khác.
→ TẢI ĐẦY ĐỦ TÀI LIỆU XUỐNG




#8. Đếm số điểm cực trị dựa vào bảng biến thiên hoặc đồ thị của hàm số
| Thông tin tài liệu | |
| Tác giả | Nhóm WORD |
| Số trang | 14 |
| Lời giải chi tiết | Có |
Mục lục tài liệu:
– Kiến thức cần nhớ
– Bài tập mẫu
– Bài tập vận dụng
→ TẢI ĐẦY ĐỦ TÀI LIỆU XUỐNG

Qua bài học hôm nay, mong rằng VerbaLearn đã giúp bạn đọc có thể nắm vững hơn về kiến thức cực trị của hàm số. Đây là một mảng kiến thức rộng và có nhiều dạng bài tập khác nhau. Để học tốt ngoài nắm chắc lý thuyết thì người học cần phải có thời gian rèn luyện bài tập để tiếp xúc với nhiều dạng nhất có thể.
BÀI HỌC TIẾP THEO
– Đường tiệm cận
– Khảo sát sự biến thiên và vẽ đồ thị hàm số
– Công thức logarit
– Công thức nguyên hàm
– Công thức tích phân















