Khái niệm lũy thừa
1. Lũy thừa với số mũ nguyên
Cho a ∈ ℝ, n ∈ ℕ* . Khi đó: ![]()
2. Lũy thừa với số mũ nguyên âm, lũy thừa với số mũ 0
Cho a ≠ 0, n ∈ ℕ* , quy ước:
Chú ý:
00 và 0-n không có nghĩa
Người ta thường dùng các lũy thừa của 10 với số mũ nguyên để biểu thị những số rất lớn và những số rất bé. Chẳng hạn: Khối lượng của Trái Đất là 5,97.1024 kg; khối lượng nguyên tử của hiđrô là 1,66.10-24 kg .
3. Căn bậc n
Khái niệm
Cho số thực b và số nguyên dương n ≥ 2. Số a được gọi là căn bậc n của số b nếu an = b
Khi n lẻ và b ∈ ℝ: Tồn tại duy nhất căn bậc n của b , kí hiệu
Khi n chẵn:
b < 0: Không tồn tại căn bậc n của b
b = 0: Có một căn bậc n của b , kí hiệu
b > 0: Có hai căn bậc n của b trái dấu, kí hiệu giá trị dương là
, còn giá trị âm là
Tính chất của căn bậc n
Với hai số không âm a, b; hai số nguyên dương m, n ta có:
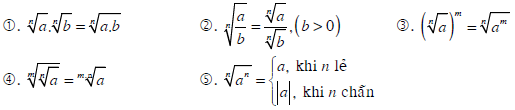
Lũy thừa với số mũ hữu tỉ
Cho số thực a > 0 và số hữu tỉ
, trong đó m ∈ ℤ, n ∈ ℕ, n ≥ 2.
Lũy thừa của a với số mũ r là số ar xác định bởi:
Lũy thừa với số mũ vô tỉ
Giả sử a là một số dương, α là một số vô tỉ và (rn) là một dãy số hữu tỉ sao cho
Khi đó:
Tính chất của lũy thừa với số mũ thực
Cho a, b là những số thực dương; α, β là những số thực tùy ý. Khi đó, ta có:
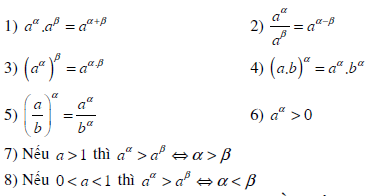
Bài tập vận dụng công thức lũy thừa
Dạng 1. Tính các giá trị của một biểu thức – Rút gọn biểu thức.
Bài 1. Tính các biểu thức sau:
Hướng dẫn giải
Bài 2. Tính các biểu thức sau:
Hướng dẫn giải
Bài 3. Tính các biểu thức sau:
Hướng dẫn giải
Bài 4. Tính các biểu thức sau:
Hướng dẫn giải
Bài 5. Cho a, b là những số thực dương. Rút gọn các biểu thức sau:
Hướng dẫn giải
Bài 6. Cho a, b là những số thực dương. Rút gọn các biểu thức sau:
Hướng dẫn giải
Bài 7. Cho a, b là những số thực dương. Rút gọn các biểu thức sau:
Hướng dẫn giải
Dạng 2. Chứng minh đẳng thức, bất đẳng thức – So sánh giá trị của biểu thức
Chú ý:
Nếu a > 1 thì α < β ⇔ aα < aβ
Nếu 0 < a < 1 thì α < β ⇔ aα > aβ
Bài 1. Hãy so sánh các cặp số sau:
Hướng dẫn giải
a) Ta có
Do 12 < 18 nên
Vì cơ số a = 5 > 1 nên
b) Ta có
c) Ta có
d) Ta có
Bài 2. Hãy so sánh các cặp số sau:
Hướng dẫn giải
a) Đưa hai căn đã cho về cùng căn bậc 15, ta được:
Do 100000 > 8000 nên
b) Ta có
Do 125 < 2401 nên
c) Ta có
Do 371293 > 279841 nên
d) Ta có
Bài 3. Hãy so sánh các cặp số sau:
Hướng dẫn giải
a) Ta có
Do 8 < 9 nên
b) Ta có
c) Ta có
d) Ta có
Bài 4. Không dùng máy tính và bảng số. Chứng minh:
Hướng dẫn giải
a)
Cách 1. Ta có:
.
Tương tự:
Suy ra:
Cách 2. Đặt
. Ta cần chứng minh x = 2
Ta có:
Từ đó ta có: x3 + 3x – 14 = 0 ⇔ (x – 2)(x2 + 2x + 7) = 0 ⇔ x = 2 (vì x2 + 2x +7 > 0)
Cách 3. Ta có:
. Do đó
nếu
và
là nghiệm của phương trình X2 – 2X – 1 = 0, tức là:
Ta chứng minh đẳng thức (1). Ta có:
. Từ đó suy ra (1).
Đẳng thức (2) chứng minh tương tự. Từ (1) và (2) suy ra điều phải chứng minh.
b)
Đặt
. Ta cần chứng minh x = 3
Ta có:
⇔ x3 – 5x – 12 = 0 ⇔ (x – 3)(x2 + 3x + 4) = 0 ⇔ x = 3 (vì x2 + 3x + 4 > 0)
c)
Cách 1. Ta có:
Vì
nên
Cách 2. Ta có:
Nên
d)
Có thể giải bằng ba cách như câu a)
Đặt H68. Ta cần chứng minh x = 3
Ta có:
⇔ x3 – 3x – 18 = 0
⇔ (x – 3)(x2 + 3x + 6) = 0 ⇔ x = 3 (vì x2 + 3x + 6 > 0)
Bài tập tự luyện
Bài 1. Hãy tính:
Bài 2. Đơn giản các biểu thức sau:
Bài 3. Đơn giản các biểu thức sau:
Bài 4. Đơn giản các biểu thức sau:
Bài 5. So sánh các số:
Bài 6. Chứng minh rằng: 

Bài 7. Rút gọn các biểu thức sau:
Kết quả:
Bài 1
Bài 2
Bài 4
Bài 5
Bài 7















