Tóm tắt toàn bộ công thức logarit thương chương trình toán lớp 12 đầy đủ. Bảng công thức giúp bạn ôn lại nhanh hơn. Xem thêm các dạng bài tập được đề cập trong bài viết sẽ giúp bạn đọc hiểu hơn về logarit và vận dụng một cách đơn giản hơn.
Bảng công thức logarit
Bảng công thức logarit giúp bạn tra cứu dễ dàng khi ôn tập. Để ghi nhớ kĩ hơn các công thức này bạn có thể thực hành nhiều dạng bài tập ở phía dưới bài viết.

Định nghĩa về logarit
Cho hai số dương a, b với a ≠ 1. Số α thỏa mãn đẳng thức aα = b được gọi là logarit cơ số a của b và kí hiệu là loga b. Ta viết: α = loga b = a ⇔ aα = b
Các tính chất: Cho a, b > 0, a ≠ 1, ta có:
loga a = 1, loga 1 = 0
, loga (aα)=α
1/ Logarit của một tích
Cho 3 số dương a, b1, b2 với a ≠ 1, ta có
loga (b1b2) = loga b1 + loga b2
Logarit của một thương: Cho 3 số a, b1, b2 với a ≠ 1, ta có
Đặc biệt: với a, b > 0, a ≠ 1,
2/ Logarit của lũy thừa
Cho a, b > 0, a ≠ 1, với mọi α, ta có
loga bα = α loga b
Đặc biệt:
3/ Công thức đổi cơ số
Cho 3 số dương a, b, c với a ≠ 1, c ≠ 1 ta có:
Đặc biệt:
và
với α ≠ 0
4/ Logarit thập phân và Logarit tự nhiên
Logarit thập phân là logarit cơ số 10. Viết : log10 b = log b = lg b
Logarit tự nhiên là logarit cơ số e. Viết : loge b = ln b
Ứng dụng công thức logarit giải bài tập
Công thức logarit vận dụng vào nhiều dạng bài tập khác nhau như tìm điều kiện xác định của biểu thức chứa logarit, biến đổi biểu thứ logarit, so sách biểu thức logarit. Các bài tập này đều là nền tảng cho phần hàm số logarit mà chúng ta sẽ được tìm hiểu ở những bài học tiếp theo.
Dạng 1: Tìm điều kiện xác định của biểu thức logarit
Ghi nhớ
Biểu thức loga f(x) xác định
Chú ý rằng: Khi giải bất phương trình An > 0 cần nhớ:
n là số tự nhiên lẻ thì An > 0 ⇔ A > 0.
n là số tự nhiên chẵn thì An > 0 ⇔ A ≠ 0.
Ví dụ 1: Với giá trị nào của x thì biểu thức A = log2 (2x – 1) xác định?
A
B
C
D x ∈ (-1; + ∞)
Lời giải
Chọn A
Điều kiện xác định: 2x – 1 > 0
Ví dụ 2: Với giá trị nào của x thì biểu thức B = ln (4 – x2) xác định?
A x ∈ [-2; 2]
B x ∈ (-2; 2)
C x ∈ ℝ [-2; 2]
D x ∈ ℝ (-2; 2)
Lời giải
Chọn B
Điều kiện xác định: 4 – x2 > 0 ⇔ -2 < x < 2
Ví dụ 3: Tìm điều kiện xác định của biểu thức 

A x ∈ (2; +∞)
B x ∈ [0; +∞)
C x ∈ [0; +∞) {2}
D x ∈ (0; +∞) {2}
Lời giải
Chọn C
Biểu thức A xác định
Vậy x ∈ [0; +∞) {2}
Ví dụ 4: Tìm điều kiện xác định của biểu thức 

A
B x ∈ (0; 2)
C
D
{1}
Lời giải
Chọn D
Biểu thức D xác định
Ví dụ 5: Với giá trị nào của m thì biểu thức 
 xác định với mọi x ∈ (-3; +∞)?
xác định với mọi x ∈ (-3; +∞)?
A m > -3
B m < -3
C m ≤ -3
D m ≥ -3
Lời giải
Chọn C
Biểu thức E xác định ⇔ x – m > 0 ⇔ x > m
Để E xác định với mọi x ∈ (-3; +∞) thì m ≤ -3
Ví dụ 6: Với giá trị nào của m thì biểu thức 
 xác định với mọi x ∈ [-4; 2]?
xác định với mọi x ∈ [-4; 2]?
A m ≥ 2
B
C m > 2
D m≥ -1
Lời giải
Chọn C
Biểu thức F xác định ⇔ (3 – x)(x + 2m) > 0 ⇔ -2m < x < 3, với
Để f(x) xác định với mọi x ∈ [-4; 2] thì [-4; 2] ⊂ (-2m; 3) ⇔ -2m < -4 ⇔ m > 2
Kết hợp với điều kiện, suy ra m > 2 thoả mãn.
Ví dụ 7: Có bao nhiêu số nguyên a để biểu thức G = log2 (ax2 – 4x + 1) có nghĩa với mọi x ∈ ℝ?
A 3
B 4
C 5
D 0
Lời giải
Chọn A
Biểu thức G xác định với mọi x ∈ ℝ ⇔ ax2 – 4x + 1 > 0, ∀ x ∈ ℝ
Vì a ∈ ℤ nên a ∈ {1; 2; 3}
Dạng 2: Rút gọn và tính giá trị biểu thức logarit
Ví dụ 1: Rút gọn biểu thức 
 (a > 0, a ≠ 1, b > 0) ta được
(a > 0, a ≠ 1, b > 0) ta được
A P = a3b-2
B P = a3b
C P = a2b3
D P = ab2
Lời giải
Chọn A
HS có thể sử dụng MTCT: Gán a = 2, b = 5 ta được
và thay a = 2, b = 5 vào 4 đáp án để so sánh.
Ví dụ 2: Cho a = log25. Ta phân tích được 
 (m, n, k ∈ ℤ). Tính m2 + n2 + k2?
(m, n, k ∈ ℤ). Tính m2 + n2 + k2?
A 13
B 10
C 22
D 14
Lời giải
Chọn C
Ta có:
⇒ m = n = 3, k = 2 ⇒ m2 + n2 + k2 = 22
Ví dụ 3: Giá trị của biểu thức 
 nằm trong khoảng nào sau đây?
nằm trong khoảng nào sau đây?
A (2; 5)
B (0;1)
C (1; 3)
D (2; 3)
Lời giải
Chọn A
HS có thể sử dụng MTCT: Gán a = 2 . Tính
và thay a = 2 vào 4 đáp án để so sánh.
Ví dụ 4: Cho số thực x thỏa mãn: 
 (a > 0, a ≠ 1). Khẳng định nào sau đây đúng?
(a > 0, a ≠ 1). Khẳng định nào sau đây đúng?
A x < 0
B x > 2
C 1 < x < 2
D 0 < x < 1
Lời giải
Chọn C
Ta có:
Ví dụ 5: Cho 0 < a ≠ 1, biểu thức 
 có giá trị bằng bao nhiêu?
có giá trị bằng bao nhiêu?
A 25
B 625
C 5
D 58
Lời giải
Chọn A
Ta có:
Ví dụ 6: Tính giá trị biểu thức 

A A = 3log37
B A = log37
C A = 2log37
D A = 4log37
Lời giải
Chọn A
Ta có:
= -log37 + 2log37 + 2log37 = 3log37
Ví dụ 7: Biểu thức 
 có giá trị bằng
có giá trị bằng
A
B -2
C 1
D -1
Lời giải
Chọn D
Ta có:
HS có thể sử dụng MTCT: Chuyển máy tính về đơn vị Rad (Shift + Mode + 4). Sau đó nhập
được kết quả bằng -1.
Ví dụ 8: Cho lg x = a, ln10 = b , với 0 < x ≠ 1. Tính log10e (x) bằng
A
B
C
D
Lời giải
Chọn B
Dạng 3: Biểu diễn logarit theo các logarit đã biết
Ghi nhớ
Để giải quyết bài toán biểu diễn logarit theo các logarit đã biết, chúng ta có thể sử dụng một trong hai cách:
Cách 1: Sử dụng các tính chất của logarit.
Cách 2: Sử dụng MTCT.
Bài toán minh hoạ: Cho log23 = a, log25 = b. Biểu diễn log320 theo a, b .
A
B
C
D
Lời giải
Chọn B
Cách 1: Sử dụng các tính chất của logarit
Ta có: log320 = log3(22․5) = 2 log32 + log35
Cách 2: Sử dụng MTCT (Casio 570 hoặc Vinacal)
Bước 1: (Gán 3 giá trị log23 và log2 vào các biến A, B và C trong máy tính)
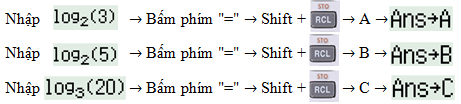
Bước 2: (Thử đáp án)

Ví dụ 1: Giả sử đặt a = log23, b = log53. Hãy biểu diễn log645 theo a và b.
A
B
C
D
Lời giải
Chọn C
Ta có
Vậy
Ví dụ 2: Giả sử đặt log126 = a, log127 = b. Hãy biểu diễn log27 theo a và b.
A
B
C
D
Lời giải
Chọn B
Cách 1: Ta có
Vậy
Cách 2: Ta có
Ví dụ 3: Cho số thực dương b thỏa mãn b ≠ 1và các số thực a, c, x thỏa mãn: logb3 = a; logb6 = c và 3x = 6. Hãy biểu diễn x theo a và c.
A
B
C a + c
D
Lời giải
Chọn D
Ta có 3x = 6 ⇔
Vậy x =
Ví dụ 4: Cho log23 = a, log35 = b, log72 = c. Hãy tính log14063 theo a, b, c
A
B
C
D
Lời giải
Chọn A
Ta có
Ví dụ 5: Cho 
 (a, b, c ∈ ℤ). Tính tổng a + b + c.
(a, b, c ∈ ℤ). Tính tổng a + b + c.
A -4
B 2
C 0
D 1
Lời giải
Chọn D
Ta có
Vậy
⇒ a + b + c = 2 – 2 + 1 = 1
Ví dụ 6: Cho các số dương a, b thỏa mãn 4a2 + 9b2 = 13ab. Chọn đẳng thức đúng trong các đẳng thức sau.
A
B
C
D
Lời giải
Chọn C
Ta có 4a2 + 9b2 = 13ab ⇔ (2x + 3b)2 = 25ab
Lấy logarit cơ số 10 cho hai vế ta được:
2log (2x + 3b) = log (25ab) ⇔ 2log (2x + 3b) = 2log5 + log a + log b
⇔
Thủ thuật casio dùng với công thức logarit
#1. Phương pháp hệ số hóa biến
– Bước 1 : Dựa vào hệ thức điều kiện buộc của đề bài chọn giá trị thích hợp cho biến
– Bước 2 : Tính các giá trị liên quan đến biến rồi gắn vào A, B, C nếu các giá trị tính được lẻ
– Bước 3 : Quan sát 4 đáp án và chọn đáp án chính xác
Một số bài toán minh họa
Bài toán 1: Đặt a = log23, b = log53. Hãy biểu diễn log645 theo a và b
A
B
C
D
Lời giải
Chọn C
#2. Phương pháp casio
Tính giá trị của a = log23. Vì giá trị của a ra một số lẻ vậy ta lưu a vào A
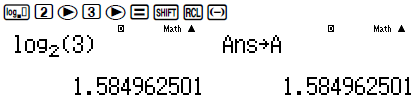
Tính giá trị của b = log53 và lưu vào B
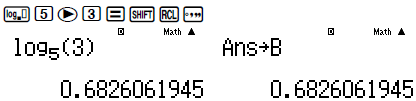
Bắt đầu ta kiểm tra tính đúng sai của đáp án A. Nếu đáp án A đúng thì hiệu
phải bằng 0. Ta nhập hiệu trên vào máy tính Casio và bấm nút =

Kết quả hiển thị của máy tính Casio là 1 giá trị khác 0 vậy đáp án A sai
Tương tự như vậy ta kiểm tra lần lượt từng đáp án và ta thấy hiệu
bằng 0

Vậy
#3. Phương pháp tự luận
Ta có
Vậy
Bình luận
Cách tự luận trong dạng bài này chủ yếu để kiểm tra công thức đổi cơ số:
Công thức 1:
(với a ≠ 1)
Công thức 2:
(với b > 0, b ≠ 1)
Cách Casio có vẻ nhiều thao tác nhưng dễ thực hiện và độ chính xác 100%. Nếu tự tin cao thì làm tự luận, nếu tự tin thấp thì nên làm Casio vì làm tự luận mà biến đổi sai 1 lần thôi rồi làm lại thì thời gian còn tốn hơn cả làm theo Casio
Bài toán 2: Cho log9 x = log12 y = log16 (x + y). Giá trị của tỉ số 
 là ?
là ?
A
B
C 1
D 2
Lời giải
Chọn B
Phương pháp casio
Từ đẳng thức log9 x = log12 y ⇒
. Thay vào hệ thức log9 x = log16 (x + y) ta được:
Ta có thể dò được nghiệm phương trình
bằng chức năng SHIFT SOLVE

Lưu nghiệm này vào giá trị A
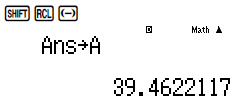
Ta đã tính được giá trị x vậy dễ dàng tính được giá trị
. Lưu giá trị y này vào biến B
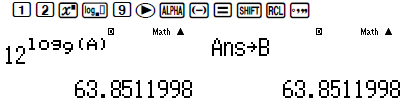
Tới đây ta dễ dàng tính được tỉ số
.

Đây chính là giá trị
Phương pháp tự luận
Đặt log9 x = log12 y = log16 (x + y) = t
Vậy x = 9t; y = 12t; x + y = 16t
Ta thiết lập phương trình
và
Vậy
Vì
> 0 nên
Bình luận
Một bài toán cực khó nếu tính theo tự luận. Nhưng nếu xử lý bằng Casio thì cũng tương đối dễ dàng và độ chính xác là 100%
Bài toán 3: Cho log2 (log8 x) = log8 (log2 x) thì (log2 x)2 bằng?
A 3
B
C 27
D
Lời giải
Chọn C
Phương trình điều kiện ⇔ log2 (log8 x) – log8 (log2 x) = 0. Dò nghiệm phương trình, lưu vào A
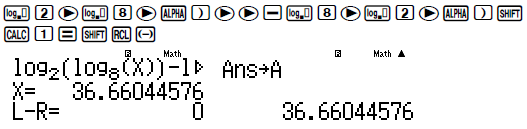
Thế x = A để tính (log2 x)2
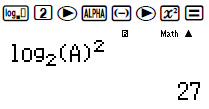
Bài toán 4: Nếu log126 = a, log127 = b thì:
A
B
C
D
Lời giải
Chọn B
Tính log126 rồi lưu vào A
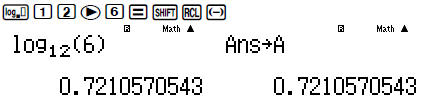
Tính log127 rồi lưu vào B
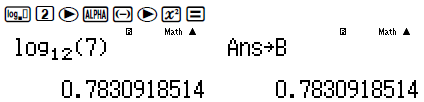
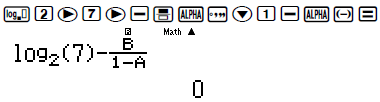
Ta thấy
Bài toán 5: Tìm x biết log3 x = 4log3 a + 7log3 b.
A x = a3b7
B x = a4b7
C x = a4b6
D x = a3b6
Lời giải
Chọn B
Theo điều kiện tồn tại của hàm logarit thì ta chọn a, b >0. Ví dụ ta chọn a = 1.125 và b = 2.175
Khi đó log3 x = 4log3 a + 7log3 b
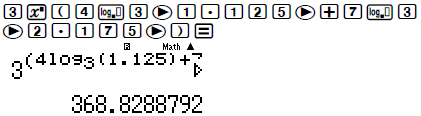
Thử các đáp án ta thấy x = (1.125)4(1.175)7
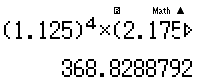
Bài toán 6: Cho hàm số 
 . Khẳng định nào sau đây đúng?
. Khẳng định nào sau đây đúng?
A y’ + 2y ln2 = 0
B y’ + 3y ln2 = 0
C y’ – 8h ln2 = 0
D y’ + 8y ln2 = 0
Lời giải
Chọn B
Chọn x = 1.25 tính
rồi lưu vào A

Tính y’(1.25) rồi lưu vào B
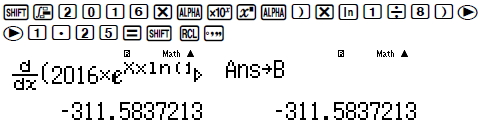
Rõ ràng B + 3 ln2․A = 0
Bài toán 7: Cho a, b > 0; a2 + b2 = 1598ab. Mệnh đề đúng là
A
B
C
D
Lời giải:
Chọn a = 2 ⇒ Hệ thức trở thành 4 + b2 = 3196b ⇔ b2 – 3196b + 4 = 0. Dò nghiệm và lưu vào B
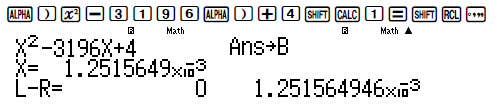
Tính
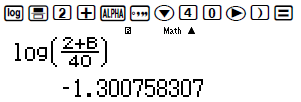
Tính tiếp log a + log b
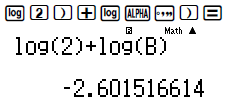
Rõ ràng giá trị log a + log b gấp 2 lần giá trị















